题目内容
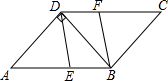 如图,在平行四边形ABCD中,∠A=60°,AD=6,且AD⊥BD,点E,F分别是边AB,CD上的动点,且AE=CF.
如图,在平行四边形ABCD中,∠A=60°,AD=6,且AD⊥BD,点E,F分别是边AB,CD上的动点,且AE=CF.(1)求证:四边形DEBF是平行四边形;
(2)当AE为何值时,四边形DEBF是矩形.
考点:矩形的判定,平行四边形的判定与性质
专题:
分析:(1)根据平行四边形的对边平行且相等可得AB∥CD,AB=CD,再求出BE=DF,然后根据一组对边平行且相等的四边形是平行四边形证明;
(2)过D作DE⊥AB于E,根据直角三角形两锐角互余求出∠ADE=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得AE=
AD.
(2)过D作DE⊥AB于E,根据直角三角形两锐角互余求出∠ADE=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得AE=
| 1 |
| 2 |
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴AB-AE=CD-CF,
∴BE=DF,BE∥DF,
∴四边形DEBF是平行四边形;
(2)解:当AE=3时,四边形DEBF是矩形.
理由是:过D作DE⊥AB于E,
则∠ADE=30°,
∴AE=AB=3,
即当AE=3时,∠DEB=∠DEA=90°,
即平行四边形BEDF是矩形;
即当AE=3时,四边形DEBF是矩形.
∴AB∥CD,AB=CD,
∵AE=CF,
∴AB-AE=CD-CF,
∴BE=DF,BE∥DF,
∴四边形DEBF是平行四边形;
(2)解:当AE=3时,四边形DEBF是矩形.

理由是:过D作DE⊥AB于E,
则∠ADE=30°,
∴AE=AB=3,
即当AE=3时,∠DEB=∠DEA=90°,
即平行四边形BEDF是矩形;
即当AE=3时,四边形DEBF是矩形.
点评:本题考查了矩形的判定,平行四边形的判定与性质,直角三角形30°角所对的直角边等于斜边的一半,熟记各性质与矩形的判定方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
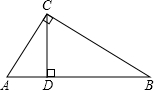 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AC=2
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AC=2| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,A点的坐标为(2,3),那么C点坐标可记为
如图,A点的坐标为(2,3),那么C点坐标可记为