题目内容
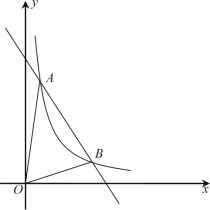
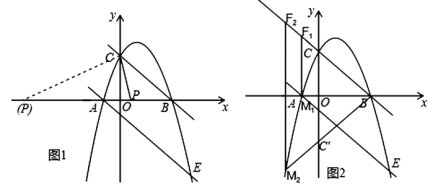
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() .
.
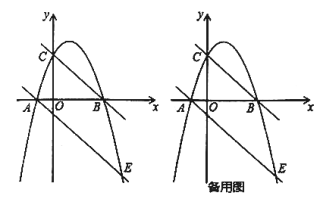
(1)求抛物线的函数表达式;
(2)抛物线与直线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 点在
点在![]() 轴上且位于点
轴上且位于点![]() 的左侧,若以
的左侧,若以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
(3)![]() 是直线
是直线![]() 上一动点,
上一动点,![]() 为抛物线上一动点,若
为抛物线上一动点,若![]() 为等腰直角三角形,请直接写出点
为等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)根据对称轴的特点,找到B的坐标,把A、B、C三点坐标代入解析式,便可求解.
(2)直线![]() 和抛物线的函数关系式成方程组,求出E的坐标,计算出AE的长度,以
和抛物线的函数关系式成方程组,求出E的坐标,计算出AE的长度,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,故分情况讨论
相似,故分情况讨论![]() 或
或![]() 从而找到P的坐标.
从而找到P的坐标.
(3)存在两种情况:
①取点![]() 与点
与点![]() 重合,过点
重合,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,
,
由![]() ,
,![]() ,找到M的坐标.
,找到M的坐标.
②取点![]() ,连接
,连接![]() ,延长
,延长![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,根据对称和平行关系找到直线
,根据对称和平行关系找到直线![]() 的函数关系式
的函数关系式
联立直线![]() 和抛物线的函数关系式成方程组,求出点
和抛物线的函数关系式成方程组,求出点![]() 的坐标.
的坐标.
(1)抛物线的对称轴是直线![]() ,且过点
,且过点![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
将![]() 、
、![]() 、
、![]() 代入
代入![]() ,得:
,得:
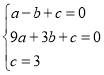 ,解得:
,解得: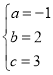 ,
,
∴抛物线的函数表达式为![]() .
.
(2)联立直线![]() 和抛物线的函数关系式成方程组,得:
和抛物线的函数关系式成方程组,得:![]() ,
,
解得: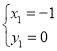 ,
,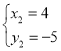 ,∴点
,∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() .
.
∵点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,∴
,∴![]() ,
,![]() .
.
∵直线![]() 的函数表达式为
的函数表达式为![]() ,∴
,∴![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
∵以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,∴
相似,∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,解得:
,解得:![]() 或
或![]() ,
,
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
∵![]() ,∴存在两种情况(如图2).
,∴存在两种情况(如图2).
①取点![]() 与点
与点![]() 重合,过点
重合,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,∴此时
,∴此时![]() 为等腰直角三角形,
为等腰直角三角形,
∴点![]() 的坐标为
的坐标为![]() ;
;
②取点![]() ,连接
,连接![]() ,延长
,延长![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,
,
∵点![]() 、
、![]() 关于
关于![]() 轴对称,
轴对称,![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∵![]() 轴,∴
轴,∴![]() 为等腰直角三角形.
为等腰直角三角形.
∵点![]() ,点
,点![]() ,∴直线
,∴直线![]() 的函数关系式为
的函数关系式为![]() ,
,
联立直线![]() 和抛物线的函数关系式成方程组,得:
和抛物线的函数关系式成方程组,得:![]() ,
,
解得: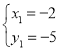 ,
,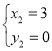 ,∴点
,∴点![]() 的坐标为
的坐标为![]() .
.
综上所述:点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

【题目】为了了解某校七年级学生每周上网的时间,甲、乙两名学生进行了抽样调查.甲同学调查了七年级电脑爱好者中40名学生每周上网的时间;乙同学从全校800名七年级学生中随机抽取了40名学生,调查了每周上网的时间.甲、乙同学各自整理的样本数据如表:
上网时间t(小时/周) | 甲学生抽样人数(人) | 乙学生抽样人数(人) |
0≤t<1.5 | 6 | 22 |
1.5≤t<2.5 | 10 | 10 |
2.5≤t<3.5 | 16 | 6 |
t≥3.5 | 8 | 2 |
(1)你认为哪名学生抽取的样本不合理,请说明理由.
(2)请你根据抽取样本合理的学生的数据,将调查结果绘制成合适的统计图(绘制一种即可).
(3)专家建议每周上网2.5小时以上(含2.5小时)的学生应适当减少上网的时间,估计该校全体七年级学生中应适当减少上网的时间的人数.
【题目】根据《N家学生体质健康标准》规定:九年级男生坐位体前屈达到17.8厘米及以上为优秀;达到13.8厘米至17.7厘米为良好;达到-0.2厘米至13.7厘米为及格;达到-0.3厘米及以下为不及格,某校为了了解九年级男生的身体柔韧性情况,从该校九年级男生中随机抽取了20%的学生进行坐位体前屈测试,并把测试结果绘制成如图所示的统计表和扇形统计图(部分信息不完整),请根据所给信息解答下列问题.
某校九年级若干男生坐位体前屈成绩统计表
成绩(厘米) | 等级 | 人数 |
≥17.8 | 优秀 |
|
13.8~17.7 | 良好 |
|
0.2~13.7 | 及格 | 15 |
≤-0.3 | 不及格 |
|
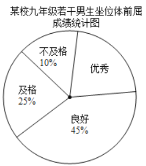
(1)求参加本次坐位体前屈测试的人数;
(2)求a,b,c的值;
(3)试估计该年级男生中坐位体前屈成绩不低于13.8厘米的人数.