题目内容
5.先化简,再求值:$\frac{a-3}{3{a}^{2}-6a}$÷(a+2-$\frac{5}{a-2}$),其中a是方程x2+3x-1=0的解.分析 先根据分式混合运算的法则把原式进行化简,再根据a是方程x2+3x-1=0的解得出a2=1-3a,代入原式进行计算即可.
解答 解:原式=$\frac{a-3}{3a(a-2)}$÷$\frac{{a}^{2}-4-5}{a-2}$
=$\frac{a-3}{3a(a-2)}$•$\frac{a-2}{(a+3)(a-3)}$
=$\frac{1}{3a(a-3)}$
=$\frac{1}{3{a}^{2}-9a}$,
∵a是方程x2+3x-1=0的解,
∴a2+3a-1=0,即a2=1-3a,
∴原式=$\frac{1}{3(1-3a)-9a}$=$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
15.下列属于最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+{b}^{2}}$ | B. | $\sqrt{\frac{1}{b}}$ | C. | $\sqrt{0.1}$ | D. | $\sqrt{18}$ |
16.若4个数6,x,8,10的中位数为7,则x的取值范围是( )
| A. | x=6 | B. | x=7 | C. | x≤6 | D. | x≥8 |
17.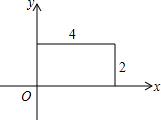 如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
 如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )| A. | (4,0) | B. | (2,4) | C. | (0,2) | D. | (4,2) |
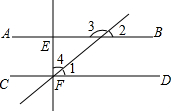 如图,AB∥CD,∠3:∠2=3:2,EF⊥CD,求∠4的度数.
如图,AB∥CD,∠3:∠2=3:2,EF⊥CD,求∠4的度数.