题目内容
13.若z=3x(3y-x)-(4x-3y)(x+3y)(1)若x,y均为整数,求证:当x是3的倍数时,z能被9整除;
(2)若y=x+1,求z的最小值.
分析 (1)首先利用整式的乘法计算方法计算,进一步合并求证得出答案即可;
(2)把y=x+1代入(1)中,整理利用二次函数的性质解决问题.
解答 解:(1)证明:
z=3x(3y-x)-(4x-3y)(x+3y)
=9xy-3x2-(4x2+9xy-9y2)
=9xy-3x2-4x2-9xy+9y2
=-7x2+9y2
∵x是3的倍数时,
∴z能被9整除.
(2)当y=x+1时,
则z=-7x2+9(x+1)2
=2x2+18x+9
=2(x+$\frac{9}{2}$)2-$\frac{63}{2}$
∵2(x+$\frac{9}{8}$)2≥0
∴z的最小值是-$\frac{63}{2}$.
点评 此题考查二次函数的性质,整式的混合运算,利用整式的计算方法先化简是解决问题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
3.据报道,某小区改进用水设备,在十年内帮助该住小区的居民累计节水1800000吨.将1800000用科学记数法表示应为( )
| A. | 0.18×107 | B. | 1.8×106 | C. | 1.8×107 | D. | 18×105 |
4.-2的绝对值等于( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
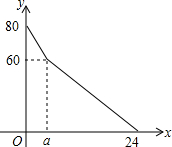 超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.
超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.