题目内容
13.解下列方程及不等式.(1)解不等式组并把解集在数轴上表示出来.$\left\{\begin{array}{l}3({x+1})>5x+4\\ \frac{x-1}{2}≤\frac{2x-1}{3}\end{array}\right.$
(2)${({\frac{x-1}{x}})^2}-14=\frac{5x-5}{x}$.
分析 (1)分别求出各不等式的解集,再求出其公共解集并在数轴上表示出来即可;
(2)先令$\frac{x-1}{x}$=y,把原方程化为关于y的一元二次方程,求出y的值,进而可得出x的值.
解答 解:(1)$\left\{\begin{array}{l}3(x+1)>5x+4①\\ \frac{x-1}{2}≤\frac{2x-1}{3}②\end{array}\right.$,由①得,x<-$\frac{1}{2}$,
由②得,x≥-1,故不等式组的解集为:-1≤x<-$\frac{1}{2}$.
在数轴上表示为: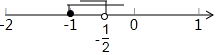 ;
;
(2)原方程可化为($\frac{x-1}{x}$)2-14=$\frac{5(x-1)}{x}$,
令$\frac{x-1}{x}$=y,则原方程可化为y2-14=5y,即(y+2)(y-7)=0,解得y=-2或y=7,
当y=-2时,$\frac{x-1}{x}$=-2,解得x=$\frac{1}{3}$;
当y=7时,$\frac{x-1}{x}$=7,解得x=-$\frac{1}{6}$,
综上所述,x1=$\frac{1}{3}$,x2=-$\frac{1}{6}$.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
1.下列命题:
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直平分且相等的四边形是正方形
④一组对边相等,另一组对边平行的四边形是平行四边形
其中正确的有( )
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直平分且相等的四边形是正方形
④一组对边相等,另一组对边平行的四边形是平行四边形
其中正确的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.某课外兴趣小组为了解所在地区的老年人的健康状况,分别作了四种不同的抽样调查,你认为抽样较合理的是( )
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 在医院调查了1000名老年人的健康状况 | |
| C. | 调查了100名小区内老年邻居的健康状况 | |
| D. | 利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 |
18.计算(-8)×3÷(-2)2得( )
| A. | -6 | B. | 6 | C. | -12 | D. | 12 |
2.正方形一边上任意一点到这个正方形两条对角线的距离之和等于对角线的( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 2倍 |
 如图,等边三角形ABC的边长为6cm,动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、PN,垂足分别为点M、N.设P、Q两点运动时间为t秒(0<t<3),四边形MNQP的面积为S cm2.
如图,等边三角形ABC的边长为6cm,动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、PN,垂足分别为点M、N.设P、Q两点运动时间为t秒(0<t<3),四边形MNQP的面积为S cm2.