题目内容
17.如图,对线段AB进行如下操作:在AB上取点P1,使得BP1=$\frac{1}{2}$AB-1,再在BP1上取点P2,使得BP2=$\frac{1}{2}$BP1-1,…,如此继续下去: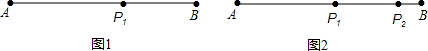
(1)如果P1P2=1,求AB的长;
(2)如果AB=6,且Pn-1Pn=1,求n的值;
(3)如果P2014P2015=1,请直接写出AB的长.
分析 (1)根据BP1=$\frac{1}{2}$AB-1和BP2=$\frac{1}{2}$BP1-1,得出P1P2=$\frac{1}{2}(\frac{1}{2}AB-1)-1$,得出AB即可.
(2)由(1)可得Pn-1Pn=$\frac{1}{{2}^{n-1}}(\frac{1}{2}AB-1)-1$,再根据AB=6,Pn-1Pn=1,解答即可.
(3)由(1)可得Pn-1Pn=$\frac{1}{{2}^{n-1}}(\frac{1}{2}AB-1)-1$,再根据P2014P2015=1,解答即可.
解答 解:(1)因为BP1=$\frac{1}{2}$AB-1,BP2=$\frac{1}{2}$BP1-1,
可得P1P2=BP1-BP2=$\frac{1}{2}(\frac{1}{2}AB-1)-1$=1,
解得:AB=10;
(2)由(1)可得Pn-1Pn=$\frac{1}{{2}^{n-1}}(\frac{1}{2}AB-1)-1$,
因为AB=6,Pn-1Pn=1,
所以可得:n=1;
(3)由(1)可得Pn-1Pn=$\frac{1}{{2}^{n-1}}(\frac{1}{2}AB-1)-1$,
因为P2014P2015=1,
所以可得:AB=22015+2.
点评 此题考查两点间的距离,关键是得出Pn-1Pn=$\frac{1}{{2}^{n-1}}(\frac{1}{2}AB-1)-1$的关系式.

练习册系列答案
相关题目
2.-4.5×10-5表示( )
| A. | -000045 | B. | -0.000045 | C. | -450000 | D. | -45000 |
6.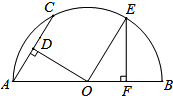 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 4 |
7.能说明命题“关于x的一元二次方程x2+mx+4=0,当m<-2时必有实数解”是假命题的一个反例为( )
| A. | m=-4 | B. | m=-3 | C. | m=-2 | D. | m=4 |
 已知正方形的边长为a,内有一个内接圆,求阴影面积.
已知正方形的边长为a,内有一个内接圆,求阴影面积.