题目内容
15.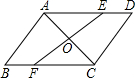 如图,AC是?ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
如图,AC是?ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.(1)求证:△AOE≌△COF;
(2)当EF与AC满足什么条件时,四边形AFCE是菱形?并说明理由.
分析 (1)由平行四边形的性质得出AD∥BC,得出∠EAO=∠FCO,由ASA即可得出结论;
(2)由△AOE≌△COF,得出对应边相等AE=CF,证出四边形AFCE是平行四边形,再由对角线EF⊥AC,即可得出四边形AFCE是菱形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵O是OA的中点,
∴OA=OC,
在△AOE和△COF中,$\left\{\begin{array}{l}{∠EAO=∠FCO}&{\;}\\{OA=OC}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$,
∴△AOE≌△COF(ASA);
(2)解:EF⊥AC时,四边形AFCE是菱形;理由如下:
∵△AOE≌△COF,
∴AE=CF,
∵AE∥CF,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形.
点评 本题考查了平行四边形的性质与判定、全等三角形的判定与性质、菱形的判定;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
5.在平面直角坐标系中,将直线l1:y=-2x-2平移后,得到直线l2:y=-2x+4,则下列平移作法正确的是( )
| A. | 将l1向右平移3个单位长度 | B. | 将l1向右平移6个单位长度 | ||
| C. | 将l1向上平移2个单位长度 | D. | 将l1向上平移4个单位长度 |
3.下列图案是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.在下列的四个几何体中,其主视图与俯视图相同的是( )
| A. | 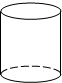 圆柱 | B. | 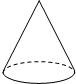 圆锥 | C. |  三棱柱 | D. | 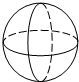 球 |
 解不等式组$\left\{\begin{array}{l}{2(x-1)≤-1①}\\{2x+3>1②}\end{array}\right.$,并把它的解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{2(x-1)≤-1①}\\{2x+3>1②}\end{array}\right.$,并把它的解集在数轴上表示出来.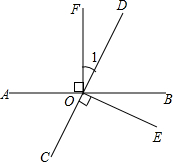 如图所示,已知∠1=40°,OE⊥CD,OF⊥AB,求∠BOE的度数.
如图所示,已知∠1=40°,OE⊥CD,OF⊥AB,求∠BOE的度数.