题目内容
19.已知:数轴上A、B两点表示的有理数分别为a、b,且(a-1)2+|b+2|=0(1)求(a+b)2016的值.
(2)数轴上的点C与A、B两点的距离的和为7,求点C在数轴上表示的数c的值.

分析 (1)根据非负数的性质列方程求出a、b的值,然后代入代数式进行计算即可得解;
(2)分点C在点B的左侧或点C在点A的右侧两种情况列方程求解即可.
解答 解:(1)∵(a-1)2+|b+2|=0,
∴a-1=0,b+2=0,
解得a=1,b=-2,
∴(a+b)2015=(1-2)2015=(-1)2015=-1;
(2)∵a=1,b=-2,数轴上A、B两点表示的有理数分别为a、b,数轴上的点C与A、B两点的距离的和为7,
∴点C可能在点B的左侧或点C可能在点A的右侧,
当点C在点B的左侧时,1-c+-2-c=7,得c=-4,
当点C在点A的右侧时,c-1+c-(-2)=7,得c=3,
即点C在数轴上表示的数c的值是-4或3.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0;还考查了数轴,难点在于分情况讨论.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.一个正比例函数的图象经过点(-2,4),它的表达式为( )
| A. | y=-2x | B. | y=2x | C. | y=-$\frac{1}{2}$x | D. | y=$\frac{1}{2}$x |
4.已知2是关于x的方程x2-2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为( )
| A. | 10 | B. | 14 | C. | 10或14 | D. | 8或10 |
8.在直角坐标系中,点P(-3,2)向右平移4个单位长度后的坐标为( )
| A. | (-3,6) | B. | (1,6) | C. | (1,2) | D. | (4,2) |
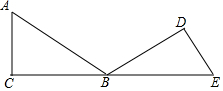 如图,在△ABC 中,∠ACB=90°,∠ABC=30°,将△ABC 绕顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
如图,在△ABC 中,∠ACB=90°,∠ABC=30°,将△ABC 绕顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.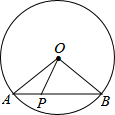 如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是60°或120°.
如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是60°或120°.