题目内容
7.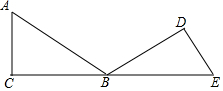 如图,在△ABC 中,∠ACB=90°,∠ABC=30°,将△ABC 绕顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
如图,在△ABC 中,∠ACB=90°,∠ABC=30°,将△ABC 绕顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.(1)求旋转角的度数;
(2)连接CD,判断△CBD的形状,并求出∠BDC的度数.
分析 (1)利用旋转的性质得到∠ABE等于旋转角,然后利用互补计算出∠ABE即可;
(2)先利用旋转的性质得BC=BD,∠CBD=∠ABE=150°,则可判断△BCD为等腰三角形,然后利用三角形内角和定理计算∠BDC的度数.
解答 解:(1)∵∠ABC=30°,
∴∠ABE=180°-30°=150°,
∵△ABC 绕顶点B顺时针旋转,使得点A与CB的延长线上的点E 重合,
重合,
∴∠ABE等于旋转角,
即旋转角的度数为150°;
(2)∵△ABC 绕顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,
∴BC=BD,∠CBD=∠ABE=150°,
∴△BCD为等腰三角形,∠BDC=$\frac{1}{2}$(180°-150°)=15°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
18.若-2xym和xny3是同类项,则m和n的值分别为( )
| A. | m=1,n=1 | B. | m=1,n=3 | C. | m=3,n=1 | D. | m=3,n=3 |
15.650万用科学记数法表示应是( )
| A. | 0.65×107 | B. | 6.5×106 | C. | 65×105 | D. | 65×106 |
12.已知m是方程2x2-x-1=0的一个根,则代数式6m2-3m的值等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.下列说法中,正确的是( )
| A. | $\sqrt{16}$=±4 | B. | -22的平方根是±2 | ||
| C. | 64的立方根是±4 | D. | -$\sqrt{5}$是5的一个平方根 |




