Question

15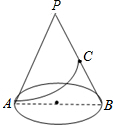．己知底面半径是4cm，母线长为12cm，C为母线PB中点，现在有一只蚂蚁从底边一点A出发．在侧面爬行到C点，则蚂蚁在圆锥侧面爬行最短距离6$\sqrt{3}$cm．

Answer 1

分析 最短距离的问题首先应转化为圆锥的侧面展开图的问题，转化为平面上两点间的距离的问题．需先算出圆锥侧面展开图的扇形半径．看如何构成一个直角三角形，然后根据勾股定理进行计算．

解答 解：圆锥的底面周长是2π×2=8π，则8π=$\frac{nπ×12}{180}$，
∴n=120°，
即圆锥侧面展开图的圆心角是120度．
∴∠APB=60°，
∵PA=PB，
∴△PAB是等边三角形，
∵C是PB中点，
∴AC⊥PB，
∴∠ACP=90度．
∵在圆锥侧面展开图中AP=12，PC=6，
∴在圆锥侧面展开图中AC=$\sqrt{A{P}^{2}-P{C}^{2}}$=6$\sqrt{3}$（cm）．
最短距离是6$\sqrt{3}$cm．
故答案为：6$\sqrt{3}$cm．

点评 本题考查了圆锥的计算，需注意最短距离的问题最后都要转化为平面上两点间的距离的问题．