题目内容
1.(1)计算:${(\frac{1}{2})^{-1}}$+4cos60°-|-3|+$\sqrt{9}$(2)解方程:x2-6x-4=0.
分析 (1)原式第一项利用负整数指数幂法则计算,第二项利用特殊角的三角函数值,第三项利用绝对值的代数意义化简,最后一项利用算术平方根定义计算即可得到结果;
(2)方程利用配方法求出解即可.
解答 解:(1)原式=2+4×$\frac{1}{2}$-3+3=2+2=4;
(2)方程整理得:x2-6x=4,
配方得:x2-6x+9=13,即(x-3)2=13,
解得:x1=3+$\sqrt{13}$,x2=3-$\sqrt{13}$.
点评 此题考查了实数的运算,以及解一元二次方程-配方法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
12.如果三角形的两条边分别为8和6,那么连接该三角形三边中点所得的周长可能是下列数据中的( )
| A. | 8 | B. | 10 | C. | 14 | D. | 16 |
10.下列计算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (-2a2)3=8a6 | C. | 2a2+a2=3a2 | D. | a3÷a=a3 |
11.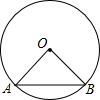 如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )
如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )
 如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )
如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )| A. | 4 | B. | 2 | C. | $2\sqrt{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
 已知实数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|a+b|-$\sqrt{(c-a)^{2}}$-2$\sqrt{{c}^{2}}$=3c-2a.
已知实数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|a+b|-$\sqrt{(c-a)^{2}}$-2$\sqrt{{c}^{2}}$=3c-2a. 如图,已知△ABC∽△AED,若∠C=60°,∠B=70°,则∠DEA=70°.
如图,已知△ABC∽△AED,若∠C=60°,∠B=70°,则∠DEA=70°.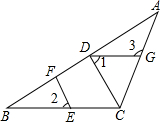 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F. 