题目内容
11.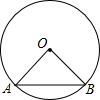 如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )
如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )| A. | 4 | B. | 2 | C. | $2\sqrt{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
分析 作OC⊥AB于C,根据垂径定理得到AC=2,根据余弦的定义列出算式计算即可.
解答 解: 作OC⊥AB于C,
作OC⊥AB于C,
则AC=$\frac{1}{2}$AB=2,
∵∠OAB=30°,
∴OA=$\frac{AC}{cos∠A}$=$\frac{2}{\frac{\sqrt{3}}{2}}$=$\frac{4\sqrt{3}}{3}$,
故选:D.
点评 本题考查的是垂径定理和锐角三角函数的应用,掌握垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
20.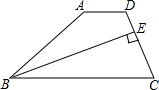 如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
 如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )| A. | $\frac{7}{4}$ | B. | $\frac{5}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
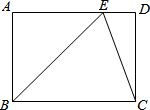 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.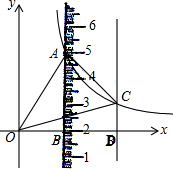 如图,平行于y轴的直尺(一部分)与双曲线y=$\frac{k}{x}$(k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm.
如图,平行于y轴的直尺(一部分)与双曲线y=$\frac{k}{x}$(k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm. 如图,若∠1=35°,则∠2=145°,∠3=35°.
如图,若∠1=35°,则∠2=145°,∠3=35°.
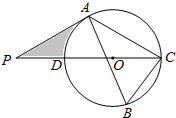 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC. 如图,函数y=x与y=$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作x轴垂线,垂足分别为点C、D,则四边形ACBD的面积为8.
如图,函数y=x与y=$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作x轴垂线,垂足分别为点C、D,则四边形ACBD的面积为8.