题目内容
如图，在正方形坐标网格中有一个圆，根据图中信息，可求得tan∠α=考点：圆周角定理,锐角三角函数的定义
专题：计算题
分析：根据圆周角定理得到∠BAC=∠α，再在Rt△ABC中，利用正切的定义得tan∠BAC=
，于是可得到tanα的值．
| 1 |
| 3 |
解答：
解：如图，
∠BAC=∠α，
在Rt△ABC中，tan∠BAC=
=
，
所以tanα=
．
故答案为
．
解：如图，∠BAC=∠α，
在Rt△ABC中，tan∠BAC=
| BC |
| AC |
| 1 |
| 3 |
所以tanα=
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了锐角三角函数．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、线段AB和线段BA是同一条线段 |
| B、射线AB和射线BA是同一条射线 |
| C、直线AB和直线BA是同一条线段 |
| D、射线AB和线段AB对应同一图形 |
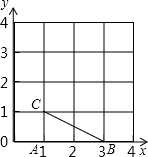如图，在直角坐标系中，△ABC是格点三角形（三角形的三个顶点都是小正方形的顶点）．函数y=a（x-1）2，y=ax+a的图象在同一坐标系的图象可能是（ ）
A、 |
B、 |
C、 |
D、 |
如图，在等腰△ABC中，顶角的平分线BD交AC于点D，AD=3，作△ABC的高AE交CB的延长线于点E，且AE与BC的长是方程组