题目内容
16．求满足下列条件的x的值：（1）4（x-2）2-25=0；
（2）8（x+5）3=-27．
分析 （1）根据平方根，即可解答；
（2）根据立方根，即可解答．
解答 解：（1）4（x-2）2-25=0
$（x-2）^{2}=\frac{25}{4}$
x-2=$±\frac{5}{2}$
解得：x=$\frac{9}{2}$或-$\frac{1}{2}$．
（2）8（x+5）3=-27
$（x+5）^{3}=\frac{-27}{8}$
x+5=-$\frac{3}{2}$
x=-$\frac{13}{2}$．
点评 本题考查了平方根、立方根，解决本题的关键是熟记平方根、立方根的定义．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
6．
如图，菱形ABCD和菱形ECGF的边长分别为4和6，∠A=120°，则图中阴影部分的面积是（ ）
如图，菱形ABCD和菱形ECGF的边长分别为4和6，∠A=120°，则图中阴影部分的面积是（ ）| A． | 8 | B． | 6 | C． | 4$\sqrt{3}$ | D． | 2$\sqrt{3}$ |
7．若x2=（-5）2，$\root{3}{{y}^{3}}$=-5，那么x+y的值是（ ）
| A． | 0 | B． | -10 | C． | 0或-10 | D． | 0或±10 |
4．若抛物线y=（x-a）2+（a-1）的顶点在第一象限，则a的取值范围为（ ）
| A． | a＞1 | B． | a＞0 | C． | a＞-1 | D． | -1＜a＜0 |
?ABCD中，M、N为BD三等分点，则EN：EF=2：3．
1．不解方程，判断一元二次方程3x2+4x-3=0的根的情况是（ ）
| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 没有实数根 | D． | 无法确定 |
8．下面说法中正确的是（ ）
| A． | -2-1-3可以说是-2，-1，-3的和 | B． | -2-1-3可以说是2，-1，-3的和 | ||
| C． | -2-1-3是连减运算不能说成和 | D． | -2-1-3=-2+3-1 |
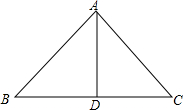如图，AB=AC，AD为△ABC的BC边上的中线，△ABD与△ACD全等吗？为什么？