题目内容
6. 如图,菱形ABCD和菱形ECGF的边长分别为4和6,∠A=120°,则图中阴影部分的面积是( )
如图,菱形ABCD和菱形ECGF的边长分别为4和6,∠A=120°,则图中阴影部分的面积是( )| A. | 8 | B. | 6 | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 如图所示:过点B作BH⊥FG,垂足为H,先证明△BCN∽△BGF,从而得到CN=2.4,于是可求得DN=1.6,然后再求得BH=5$\sqrt{3}$,从而可求得阴影部分的面积.
解答 解:过点B作BH⊥FG,垂足为H.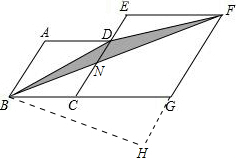
∵四边形ECGF是菱形,
∴NC∥GF.
∴△BCN∽△BGF.
∴CN:GF=CB:BG,即CN:6=4:10.
解得:CN=2.4.
∴DN=4-2.4=1.6.
由∠A=120°可知:∠BGH=∠ABG=60°.
∴BH=BG•sin60°=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$.
∴阴影部分的面积=$\frac{1}{2}×DN×BH$=$\frac{1}{2}×1.6×5\sqrt{3}$=4$\sqrt{3}$.
故选:C.
点评 本题主要考查的是相似三角形的性质和判定,求得DN和BH的长是解题的关键.

练习册系列答案
相关题目
14.下列根据等式的性质变形正确的是( )
| A. | 由4x=2x-1,得4x-2x=1 | B. | 由-2x=4,得x=2 | ||
| C. | 由5x-3=4,得5x=4-3 | D. | 由-3x-2=2x+3,得-3x-2x=3+2 |
18.在某中学开展的“书香伴我行”读书活动中,为了解九年级300名学生一个月的读书情况,随机调查了九年级50名学生读书的册数,统计数据如表所示:
估计这所中学九年级学生一个月共读书约648册,你的估计理由是50名学生读书的平均册数等于全年级学生读书的册数.
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 13 | 16 | 17 | 3 |
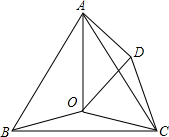 如图,点O是等边△ABC内一点,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OA和OD.
如图,点O是等边△ABC内一点,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OA和OD.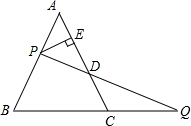 如图,P是等边△ABC的AB边上一点,过P作PE⊥AC于E,在BC的延长线上截取CQ=AP,连接PQ交AC于点D.
如图,P是等边△ABC的AB边上一点,过P作PE⊥AC于E,在BC的延长线上截取CQ=AP,连接PQ交AC于点D.