题目内容
已知一次函数y=kx+b的图象经过点(3,2)和点(-2,1).
(1)求该函数的表达式;
(2)若正比例函数y=mx与y=kx+b平行,求正比例函数表达式.
(1)求该函数的表达式;
(2)若正比例函数y=mx与y=kx+b平行,求正比例函数表达式.
考点:待定系数法求一次函数解析式,两条直线相交或平行问题
专题:计算题
分析:(1)把两个点的坐标分别代入y=kx+b得到关于k、b的方程组,然后解方程组求出k、b即可得到函数解析式;
(2)根据两直线平行的问题即可得到m=
.
(2)根据两直线平行的问题即可得到m=
| 1 |
| 5 |
解答:解:(1)根据题意得
,解得
,
所以该函数解析式为y=
x+
;
(2)因为正比例函数y=mx与y=kx+b平行,
所以m=k=
,
即正比例函数表达式为y=
.
|
|
所以该函数解析式为y=
| 1 |
| 5 |
| 7 |
| 5 |
(2)因为正比例函数y=mx与y=kx+b平行,
所以m=k=
| 1 |
| 5 |
即正比例函数表达式为y=
| 1 |
| 5 |
点评:本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况,投进的个数分别为6,10,5,3,4,8,4,这组数据的中位数和极差分别是( )
| A、4,7 | B、5,7 |
| C、7,5 | D、3,7 |
下列各数中,即大于2又小于3的数是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列计算正确的是( )
| A、x2•x4=x8 |
| B、(x3)3=x6 |
| C、x3÷x=x3 |
| D、(-2a2)3=-8a6 |

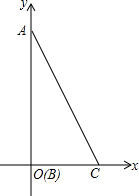 Rt△ABC中,AB=6,∠ACB=60°,∠ABC=90°.建立如图所示的平面直角坐标系xOy(点B与原点O重合,点C在x轴上).
Rt△ABC中,AB=6,∠ACB=60°,∠ABC=90°.建立如图所示的平面直角坐标系xOy(点B与原点O重合,点C在x轴上).