题目内容
2.已知整数x满足不等式组$\left\{\begin{array}{l}5-2(x-3)≥x+2\\ \frac{2x-2}{3}≤\frac{1+2x}{2}-1\end{array}\right.$,试求出x的值.分析 根据不等式组$\left\{\begin{array}{l}5-2(x-3)≥x+2\\ \frac{2x-2}{3}≤\frac{1+2x}{2}-1\end{array}\right.$,可以求得x的取值范围,从而可以确定整数x的值.
解答 解:$\left\{\begin{array}{l}{5-2(x-3)≥x+2}&{①}\\{\frac{2x-2}{3}≤\frac{1+2x}{2}-1}&{②}\end{array}\right.$
解不等式①,得x≤3,
解不等式②,得x≥-$\frac{1}{2}$,
故原不等式组的解集是$-\frac{1}{2}≤x≤3$,
即x的值是x=0或x=1或x=2或x=3.
点评 本题考查一元一次不等式组的整数解,解题的关键是明确解一元一次不等式组的方法.

练习册系列答案
相关题目
12.关于x的一元二次方程(m-1)x2+3x+m2-1=0的一根为0,则m的值是( )
| A. | -1 | B. | -2 | C. | ±1 | D. | ±2 |
14.某计算器每个定价80元,若购买不超过20个,则按原价付款:若一次购买超过20个,则超过部分按七折付款.设一次购买数量为x(x>20)个,付款金额为y元,则y与x之间的表达式为( )
| A. | y=0.7×80(x-20)+80×20 | B. | y=0.7x+80(x-10) | ||
| C. | y=0.7×80•x | D. | y=0.7×80(x-10) |
11.在方程2(x+y)-3(y-x)=3中,用含x的式子表示y,则( )
| A. | y=5x-3 | B. | y=-x-3 | C. | $y=\frac{3x-2}{2}$ | D. | y=5x+3 |
12.已知32m=10,3n=2,则92m-n的值为( )
| A. | 25 | B. | 96 | C. | 5 | D. | 3 |
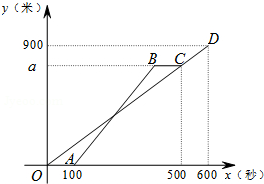 甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.
甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.