题目内容
2.第一象限内两点A(1,1)、B(5,3),点P在x轴上,且PA+PB的和为最小,则P点坐标(2,0).分析 先画出图形,由两点之间线段最短可知,作出A点对称点,当P点在线段AB上时PA+PB的值最小,即PA+PB=A′B,求得直线A′B的解析式为y=x-2,当y=0时,x=2,即可得到结论.
解答 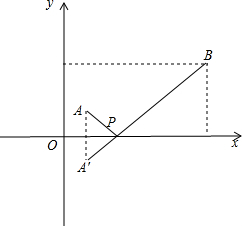 解:作点A关于x轴的对称点A',则A′坐标为(1,-1),
解:作点A关于x轴的对称点A',则A′坐标为(1,-1),
连接A′B交x轴于一点,此点就是点P,此时PA+PB最小,
作BE⊥y于一点E,延长A′A交BE于一点M,
∵PB=PA′,
∴PA+PB=BA′,
∵A、B两点的坐标分别为(1,1)和(5,3),A′坐标为(1,-1),
设直线A′B的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{-1=k+b}\\{3=5k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$
∴直线A′B的解析式为:y=x-2,
当y=0时,x=2,
∴P(2,0).
故答案为:(2,0).
点评 本题考查的是最短线路问题及用待定系数法求一次函数的解析式,熟知轴对称的性质及一次函数的相关知识是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.某超市有一种商品,进价为2元,据市场调查,销售单价是13元时,平均每天销售量是50件,而销售价每降低1元,平均每天就可以多售出10件.若设降价后售价为x元,每天利润为y元,则y与x之间的函数关系为( )
| A. | y=10x2-100x-160 | B. | y=-10x2+200x-360 | ||
| C. | y=x2-20x+36 | D. | y=-10x2+310x-2340 |
10.在3.14、-$\sqrt{2}$、$\root{3}{27}$、π、0.2020020002…这六个数中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |