题目内容
已知直线MA∥NB.
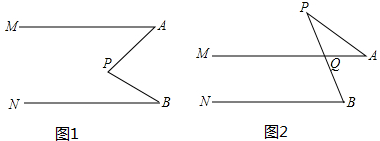
(1)如图1,点P在直线MA与NB之间,你能得到∠APB=∠A+∠B这个结论吗?并说明你的理由;
(2)如图2,若P在两条直线MA,NB之外,你仍能得到与第(1)题类似的结论吗?请说明理由.

(1)如图1,点P在直线MA与NB之间,你能得到∠APB=∠A+∠B这个结论吗?并说明你的理由;
(2)如图2,若P在两条直线MA,NB之外,你仍能得到与第(1)题类似的结论吗?请说明理由.
考点:平行线的性质
专题:
分析:(1)过P作PE∥AM,根据平行线的性质可证得结论;
(2)由平行可得到∠B=∠PQM,结合三角形的外角性质可得∠B=∠A+∠APB.
(2)由平行可得到∠B=∠PQM,结合三角形的外角性质可得∠B=∠A+∠APB.
解答:解:
(1)能.理由如下:
如图,过点P作PE∥AM,
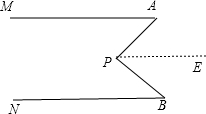
∵AM∥BN,
∴PE∥BN,
∴∠A=∠APE,∠B=∠BPE,
∴∠APB=∠APE+∠BPE=∠A+∠B.
(2)可得到∠B=∠A+∠APB,理由如下:
∵AM∥BN,
∴∠B=∠PQM,
又∠BPM=∠A+∠APB,
∴∠B=∠A+∠APB.
(1)能.理由如下:
如图,过点P作PE∥AM,

∵AM∥BN,
∴PE∥BN,
∴∠A=∠APE,∠B=∠BPE,
∴∠APB=∠APE+∠BPE=∠A+∠B.
(2)可得到∠B=∠A+∠APB,理由如下:
∵AM∥BN,
∴∠B=∠PQM,
又∠BPM=∠A+∠APB,
∴∠B=∠A+∠APB.
点评:本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
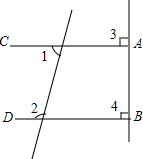 如图,已知CA⊥BA于A,DB⊥AB于B,∠1与∠2有什么关系?说明理由.
如图,已知CA⊥BA于A,DB⊥AB于B,∠1与∠2有什么关系?说明理由.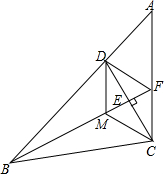 如图,在△ABC中,D是AB上一点,且BD=BC,BF⊥CD于点E,交AC于点F,M为线段BE上任意一点,请探究,当ME与EF满足什么数量关系时四边DMCF是菱形?
如图,在△ABC中,D是AB上一点,且BD=BC,BF⊥CD于点E,交AC于点F,M为线段BE上任意一点,请探究,当ME与EF满足什么数量关系时四边DMCF是菱形?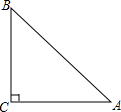 如图,在Rt△ABC中,∠C=90°,∠A=45°.若设BC=x,则AC=
如图,在Rt△ABC中,∠C=90°,∠A=45°.若设BC=x,则AC= 如图,在Rt△ABC中,∠ACB=90°,且AB=
如图,在Rt△ABC中,∠ACB=90°,且AB= 已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE.
已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE.  在数轴上画出
在数轴上画出