题目内容
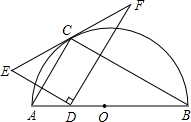 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2| 3 |
 |
| BC |
| 5 |
| 3 |
考点:圆的综合题,垂线段最短,平行线的判定与性质,等边三角形的判定与性质,含30度角的直角三角形,切线的判定,轴对称的性质,相似三角形的判定与性质
专题:压轴题
分析:(1)由点E与点D关于AC对称可得CE=CD,再根据DF⊥DE即可证到CE=CF.
(2)根据“点到直线之间,垂线段最短”可得CD⊥AB时CD最小,由于EF=2CD,求出CD的最小值就可求出EF的最小值.
(3)连接OC,易证△AOC是等边三角形,AD=OD,根据等腰三角形的“三线合一”可求出∠ACD,进而可求出∠ECO=90°,从而得到EF与半圆相切.
(4)利用相似三角形的判定与性质可证到△DBF是等边三角形,只需求出BF就可求出DB,进而求出AD长.
(5)首先根据对称性确定线段EF扫过的图形,然后探究出该图形与△ABC的关系,就可求出线段EF扫过的面积.
(2)根据“点到直线之间,垂线段最短”可得CD⊥AB时CD最小,由于EF=2CD,求出CD的最小值就可求出EF的最小值.
(3)连接OC,易证△AOC是等边三角形,AD=OD,根据等腰三角形的“三线合一”可求出∠ACD,进而可求出∠ECO=90°,从而得到EF与半圆相切.
(4)利用相似三角形的判定与性质可证到△DBF是等边三角形,只需求出BF就可求出DB,进而求出AD长.
(5)首先根据对称性确定线段EF扫过的图形,然后探究出该图形与△ABC的关系,就可求出线段EF扫过的面积.
解答: 解:①连接CD,如图1所示.
解:①连接CD,如图1所示.
∵点E与点D关于AC对称,
∴CE=CD.
∴∠E=∠CDE.
∵DF⊥DE,
∴∠EDF=90°.
∴∠E+∠F=90°,∠CDE+∠CDF=90°.
∴∠F=∠CDF.
∴CD=CF.
∴CE=CD=CF.
∴结论“CE=CF”正确.
②当CD⊥AB时,如图2所示.
∵AB是半圆的直径,
∴∠ACB=90°.
∵AB=8,∠CBA=30°,
∴∠CAB=60°,AC=4,BC=4
.
∵CD⊥AB,∠CBA=30°,
∴CD=
BC=2
.
根据“点到直线之间,垂线段最短”可得:
点D在线段AB上运动时,CD的最小值为2
.
∵CE=CD=CF,
∴EF=2CD.
∴线段EF的最小值为4
.
∴结论“线段EF的最小值为2
”错误.
③当AD=2时,连接OC,如图3所示.
∵OA=OC,∠CAB=60°,
∴△OAC是等边三角形.
∴CA=CO,∠ACO=60°.
∵AO=4,AD=2,
∴DO=2.
∴AD=DO.
∴∠ACD=∠OCD=30°.
∵点E与点D关于AC对称,
∴∠ECA=∠DCA.
∴∠ECA=30°.
∴∠ECO=90°.
∴OC⊥EF.
∵EF经过半径OC的外端,且OC⊥EF,
∴EF与半圆相切.
∴结论“EF与半圆相切”正确.
④当点F恰好落在
上时,连接FB、AF,如图4所示.
∵点E与点D关于AC对称,
∴ED⊥AC.
∴∠AGD=90°.
∴∠AGD=∠ACB.
∴ED∥BC.
∴△FHC∽△FDE.
∴
=
.
∵FC=
EF,
∴FH=
FD.
∴FH=DH.
∵DE∥BC,
∴∠FHC=∠FDE=90°.
∴BF=BD.
∴∠FBH=∠DBH=30°.
∴∠FBD=60°.
∵AB是半圆的直径,
∴∠AFB=90°.
∴∠FAB=30°.
∴FB=
AB=4.
∴DB=4.
∴AD=AB-DB=4.
∴结论“AD=2
”错误.
⑤∵点D与点E关于AC对称,
点D与点F关于BC对称,
∴当点D从点A运动到点B时,
点E的运动路径AM与AB关于AC对称,
点F的运动路径NB与AB关于BC对称.
∴EF扫过的图形就是图5中阴影部分.
∴S阴影=2S△ABC
=2×
AC•BC
=AC•BC
=4×4
=16
.
∴EF扫过的面积为16
.
∴结论“EF扫过的面积为16
”正确.
故答案为:①、③、⑤.
 解:①连接CD,如图1所示.
解:①连接CD,如图1所示.∵点E与点D关于AC对称,
∴CE=CD.
∴∠E=∠CDE.
∵DF⊥DE,
∴∠EDF=90°.
∴∠E+∠F=90°,∠CDE+∠CDF=90°.
∴∠F=∠CDF.
∴CD=CF.
∴CE=CD=CF.
∴结论“CE=CF”正确.

②当CD⊥AB时,如图2所示.
∵AB是半圆的直径,
∴∠ACB=90°.
∵AB=8,∠CBA=30°,
∴∠CAB=60°,AC=4,BC=4
| 3 |
∵CD⊥AB,∠CBA=30°,
∴CD=
| 1 |
| 2 |
| 3 |
根据“点到直线之间,垂线段最短”可得:
点D在线段AB上运动时,CD的最小值为2
| 3 |
∵CE=CD=CF,
∴EF=2CD.
∴线段EF的最小值为4
| 3 |
∴结论“线段EF的最小值为2
| 3 |
③当AD=2时,连接OC,如图3所示.

∵OA=OC,∠CAB=60°,
∴△OAC是等边三角形.
∴CA=CO,∠ACO=60°.
∵AO=4,AD=2,
∴DO=2.
∴AD=DO.
∴∠ACD=∠OCD=30°.
∵点E与点D关于AC对称,
∴∠ECA=∠DCA.
∴∠ECA=30°.
∴∠ECO=90°.
∴OC⊥EF.
∵EF经过半径OC的外端,且OC⊥EF,
∴EF与半圆相切.
∴结论“EF与半圆相切”正确.
④当点F恰好落在
 |
| BC |

∵点E与点D关于AC对称,
∴ED⊥AC.
∴∠AGD=90°.
∴∠AGD=∠ACB.
∴ED∥BC.
∴△FHC∽△FDE.
∴
| FH |
| FD |
| FC |
| FE |
∵FC=
| 1 |
| 2 |
∴FH=
| 1 |
| 2 |
∴FH=DH.
∵DE∥BC,
∴∠FHC=∠FDE=90°.
∴BF=BD.
∴∠FBH=∠DBH=30°.
∴∠FBD=60°.
∵AB是半圆的直径,
∴∠AFB=90°.
∴∠FAB=30°.
∴FB=
| 1 |
| 2 |
∴DB=4.
∴AD=AB-DB=4.
∴结论“AD=2
| 5 |
⑤∵点D与点E关于AC对称,

点D与点F关于BC对称,
∴当点D从点A运动到点B时,
点E的运动路径AM与AB关于AC对称,
点F的运动路径NB与AB关于BC对称.
∴EF扫过的图形就是图5中阴影部分.
∴S阴影=2S△ABC
=2×
| 1 |
| 2 |
=AC•BC
=4×4
| 3 |
=16
| 3 |
∴EF扫过的面积为16
| 3 |
∴结论“EF扫过的面积为16
| 3 |
故答案为:①、③、⑤.
点评:本题考查了等边三角形的判定与性质、平行线的判定与性质、相似三角形的判定与性质、切线的判定、轴对称的性质、含30°角的直角三角形、垂线段最短等知识,综合性强,有一定的难度.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
掷一枚质地均匀的硬币10次,下列说法正确的是( )
| A、可能有5次正面朝上 |
| B、必有5次正面朝上 |
| C、掷2次必有1次正面朝上 |
| D、不可能10次正面朝上 |
下列函数中,自变量x的取值范围是x>1且x≠3的是( )
A、y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
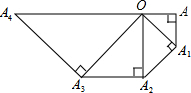 如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…则OA6的长度为
如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…则OA6的长度为 在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为
在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为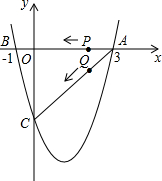 如图,二次函数y=
如图,二次函数y=