题目内容
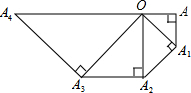 如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…则OA6的长度为
如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…则OA6的长度为考点:等腰直角三角形
专题:压轴题,规律型
分析:利用等腰直角三角形的性质以及勾股定理分别求出各边长,进而得出答案.
解答:解:∵△OAA1为等腰直角三角形,OA=1,
∴AA1=OA=1,OA1=
OA=
;
∵△OA1A2为等腰直角三角形,
∴A1A2=OA1=
,OA2=
OA1=2;
∵△OA2A3为等腰直角三角形,
∴A2A3=OA2=2,OA3=
OA2=2
;
∵△OA3A4为等腰直角三角形,
∴A3A4=OA3=2
,OA4=
OA3=4.
∵△OA4A5为等腰直角三角形,
∴A4A5=OA4=4,OA5=
OA4=4
.
∵△OA5A6为等腰直角三角形,
∴A5A6=OA5=4
,OA6=
OA5=8.
故答案为:8.
∴AA1=OA=1,OA1=
| 2 |
| 2 |
∵△OA1A2为等腰直角三角形,
∴A1A2=OA1=
| 2 |
| 2 |
∵△OA2A3为等腰直角三角形,
∴A2A3=OA2=2,OA3=
| 2 |
| 2 |
∵△OA3A4为等腰直角三角形,
∴A3A4=OA3=2
| 2 |
| 2 |
∵△OA4A5为等腰直角三角形,
∴A4A5=OA4=4,OA5=
| 2 |
| 2 |
∵△OA5A6为等腰直角三角形,
∴A5A6=OA5=4
| 2 |
| 2 |
故答案为:8.
点评:此题主要考查了等腰直角三角形的性质以及勾股定理,熟练应用勾股定理得出是解题关键.

练习册系列答案
相关题目
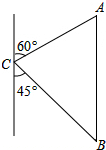 如图,有小岛A和小岛B,轮船以45km/h的速度由C向东航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据:
如图,有小岛A和小岛B,轮船以45km/h的速度由C向东航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据:
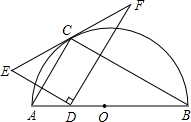 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2