题目内容
 在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为
在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为考点:轴对称-最短路线问题,一次函数图象上点的坐标特征
专题:
分析:利用一次函数图象上点的坐标性质得出OA′=1,进而利用勾股定理得出即可.
解答: 解:如图所示:作A点关于直线y=x的对称点A′,连接A′B,交直线y=x于点P,
解:如图所示:作A点关于直线y=x的对称点A′,连接A′B,交直线y=x于点P,
此时PA+PB最小,
由题意可得出:OA′=1,BO=2,PA′=PA,
∴PA+PB=A′B=
=
.
故答案为:
.
 解:如图所示:作A点关于直线y=x的对称点A′,连接A′B,交直线y=x于点P,
解:如图所示:作A点关于直线y=x的对称点A′,连接A′B,交直线y=x于点P,此时PA+PB最小,
由题意可得出:OA′=1,BO=2,PA′=PA,
∴PA+PB=A′B=
| 12+22 |
| 5 |
故答案为:
| 5 |
点评:此题主要考查了利用轴对称求最短路线以及一次函数图象上点的特征等知识,得出P点位置是解题关键.

练习册系列答案
相关题目
2013年12月2日,“嫦娥三号”从西昌卫星发射中心成功发射,在此次任务中,“嫦娥三号”要一次入轨,直接进入近地点约200000米,远地点约380 000 000米的地月转移轨道,其中380 000 000用科学记数法可以表示为( )
| A、38×107 |
| B、3.8×107 |
| C、3.8×108 |
| D、0.38×109 |

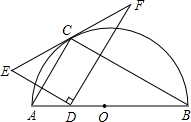 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2
 如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,且∠BAC=32°.
如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,且∠BAC=32°.