题目内容
19.先化简,再求值:($\frac{x}{x-1}$-$\frac{x}{{x}^{2}-1}$)÷$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$;其中x是不等式x-$\frac{4x-1}{3}$>1的最大整数解.分析 先化简分式,再求出不等式的解,代入求解即可.
解答 解:原式=$\frac{x(x+1)-x}{(x+1)(x-1)}×\frac{{{x^2}-2x+1}}{{{x^2}-x}}$
=$\frac{x^2}{(x+1)(x-1)}×\frac{{{{({x-1})}^2}}}{{x({x-1})}}$
=$\frac{x}{x+1}$
解这个不等式得x<-2,
x为最大整数解,∴x的值为-3,
∴原式=$\frac{3}{2}$.
点评 本题主要考查了分式的化简求值与一元一次不等式的整数解,解题的关键是正确的化简.

练习册系列答案
相关题目
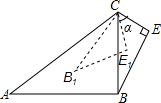 如图,在△ABC和△BCE中,∠CBE=30°,∠BEC=90°,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点F,与直线CB交于点Q,当△BPQ为等腰三角形时,α的大小是30°,75°或165°.
如图,在△ABC和△BCE中,∠CBE=30°,∠BEC=90°,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点F,与直线CB交于点Q,当△BPQ为等腰三角形时,α的大小是30°,75°或165°.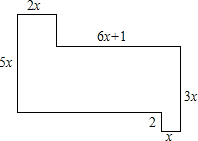 如图的面积为22x2+4x (以x来表示)
如图的面积为22x2+4x (以x来表示) 如图,点P是矩形ABCD的边AD上一动点,矩形的两条 边长AB、BC分别为8和15,则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$.
如图,点P是矩形ABCD的边AD上一动点,矩形的两条 边长AB、BC分别为8和15,则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$.