在式子$\frac{1}{a}.\frac{b}{3}.\frac{c}{a-b}.\frac{2ab}{π}.\frac{x}{{{x^2}-{y^2}}}$中.所有的式子均有意义.则分式的个数为( )A．2个B．3个C．4个D．5个题目和参考答案——青夏教育精英家教网—

题目内容

14．在式子$\frac{1}{a}，\frac{b}{3}，\frac{c}{a-b}，\frac{2ab}{π}，\frac{x}{{{x^2}-{y^2}}}$中，所有的式子均有意义，则分式的个数为（　　）

A．

2个

B．

3个

C．

4个

D．

5个

分析判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．

解答解：$\frac{b}{3}$，$\frac{2ab}{π}$的分母中均不含有字母，因此它们是整式，而不是分式．
$\frac{1}{a}$，$\frac{c}{a-b}$，$\frac{x}{{x}^{2}-{y}^{2}}$分母中含有字母，因此是分式．
故选B．

点评本题主要考查分式的定义，注意π不是字母，是常数，所以$\frac{2ab}{π}$不是分式，是整式．

练习册系列答案

相关题目

4．等腰三角形的一个内角等于40°，则它两底角的平分线所夹的钝角为（　　）

5．把一元二次方程（x+5）（3+x）=2x²化成一般形式是x²-8x-15=0；它的二次项系数是1；一次项是-8；常数项是-15．

2．计算：3x-5x=-2x，（m²）³=m⁶，a⁵•a⁵=a¹⁰．

9．

已知∠α，求作∠AOB使∠AOB=∠α．

19．如果把分式$\frac{10x}{2x+y}$中的x、y都扩大10倍，则分式的值（　　）

6．一个列数是按以下规律组成的：
$\frac{1}{1}$，$\frac{1}{2}$，$\frac{2}{1}$，$\frac{1}{3}$，$\frac{2}{2}$，$\frac{3}{1}$，$\frac{1}{4}$，$\frac{2}{3}$，$\frac{3}{2}$，$\frac{4}{1}$，$\frac{1}{5}$，$\frac{2}{4}$，$\frac{3}{3}$，$\frac{4}{2}$，$\frac{5}{1}$，$\frac{1}{6}$，…
（1）$\frac{27}{40}$是数列中的第2172项；
（2）第180项是哪个分数？$\frac{9}{10}$．

3．

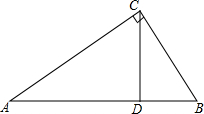如图，△ABC中，∠ACB=90°，AB=$\sqrt{8}$，BC=$\sqrt{2}$．
（1）求AC的长；
（2）求斜边AB上的高CD．

4．

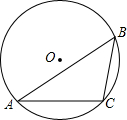如图，⊙O是△ABC的外接圆，BC=4cm，∠A=30°，求⊙O的面积（用两种不同的方法求解）．

试题分类