Question

如图，已知双曲线y=

k

x

(x＞0)经过矩形OAPB边PB中点M，交PA于点N，且四边形ONPM的面积为

3

4

，则k的值为

 

．

Answer 1

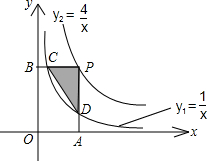
分析：如图，连接OP，那么△OPB和△OPA的面积相等，又M、N都在双曲线上，由此得到△OBM和△OAN的面积相等，又M为BP的中点，由此得到△OBM和△OPM的面积相等，然后利用已知条件即可求出k值．

解答：解：如图，连接OP，
∵矩形OAPB
∴△OPB和△OPA的面积相等，
∵又M、N都在双曲线上，
∴△OBM和△OAN的面积相等，
∵又M为BP的中点，
∴△OBM和△OPM的面积相等，
而四边形ONPM的面积为

3

4

，
∴S_△OBM=S_△OAN=

1

2

×

3

4

，
∴k=

3

4

．
故答案为：

3

4

．

点评：此题主要考查了反比例函数的图象和性质，也利用了矩形的性质，解题的关键是利用矩形的性质和已知条件求出和反比例函数图象相关的三角形的面积即可解决问题．