题目内容
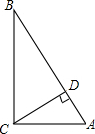 如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AD=
如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AD=| 5 |
| 5 |
考点:解直角三角形
专题:
分析:先在Rt△ACD中,由勾股定理求出AC=
=5,根据余弦函数的定义得出cosA=
=
;再由同角的余角相等得到∠B=∠ACD=90°-∠A,那么cosB=cos∠ACD=
=
;再根据tanB=tan∠ACD,得到
=
,于是BD=
=4
.
| AD2+CD2 |
| AD |
| AC |
| ||
| 5 |
| CD |
| AC |
2
| ||
| 5 |
| CD |
| BD |
| AD |
| CD |
| CD2 |
| AD |
| 5 |
解答:解:在Rt△ACD中,∵∠ADC=90°,AD=
,CD=2
,
∴AC=
=5,
∴cosA=
=
;
∵∠ACB=90°,CD⊥AB于D,
∴∠B=∠ACD=90°-∠A,
∴cosB=cos∠ACD=
=
;
∵tanB=tan∠ACD,
∴
=
,
∴BD=
=
=4
.
| 5 |
| 5 |
∴AC=
| AD2+CD2 |
∴cosA=
| AD |
| AC |
| ||
| 5 |
∵∠ACB=90°,CD⊥AB于D,
∴∠B=∠ACD=90°-∠A,
∴cosB=cos∠ACD=
| CD |
| AC |
2
| ||
| 5 |
∵tanB=tan∠ACD,
∴
| CD |
| BD |
| AD |
| CD |
∴BD=
| CD2 |
| AD |
(2
| ||
|
| 5 |
点评:本题考查了解直角三角形,勾股定理,余角的性质,锐角三角函数的定义,难度适中.利用转化思想可使解答简便.

练习册系列答案
相关题目
若x<y成立,则下列不等式成立的是( )
| A、-3x<-3y |
| B、x-2<y-2 |
| C、4x>4y |
| D、-x+2<-y+2 |
有长度分别为2cm,3cm,4cm,7cm的四条线段,任取其中三条能组成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列各组中是同类项的一组是( )
| A、xy3与-2x3y |
| B、3xy3与-2xy3z |
| C、y3与x3 |
| D、-2xy3与3y3x |
 如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有
如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有 如图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,求∠ADC的度数.
如图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,求∠ADC的度数.