题目内容
 如图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,求∠ADC的度数.
如图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,求∠ADC的度数.考点:三角形内角和定理
专题:
分析:根据角平分线的定义求出∠DAC,根据直角三角形两锐角互余求出∠ACE,再求出∠ACD,然后利用三角形的内角和等于180°列式计算即可得解.
解答:解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=30°,
∵CE是△ABC的高,
∴∠AEC=90°,
∴∠ACE=30°,
∴∠ACD=80°,
在△ACD中,∠ADC=180°-30°-80°=70°,
答:∠ADC=70°.
∴∠DAC=30°,
∵CE是△ABC的高,
∴∠AEC=90°,
∴∠ACE=30°,
∴∠ACD=80°,
在△ACD中,∠ADC=180°-30°-80°=70°,
答:∠ADC=70°.
点评:本题考查了三角形的内角和定理,角平分线的定义,熟记概念并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列结论错误的是( )
A、若a=b,则
| ||||
B、若
| ||||
| C、若x=3,则x2=3x | ||||
| D、若ax+2=bx+2,则a=b |
 如图,直线AB与CD相交于点O,已知∠DOE=75°,∠BOE=35°,求∠AOC,∠AOD的度数.
如图,直线AB与CD相交于点O,已知∠DOE=75°,∠BOE=35°,求∠AOC,∠AOD的度数.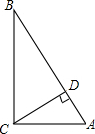 如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AD=
如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AD=