题目内容
 如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有
如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有考点:等腰三角形的判定,坐标与图形性质
专题:分类讨论
分析:分为三种情况:①OA=OP,②AP=OP,③OA=OA,分别画出即可.
解答:解:以O为圆心,以OA为半径画弧交x轴于点P和P′,此时三角形是等腰三角形,即2个;

以A为圆心,以OA为半径画弧交x轴于点P″(O除外),此时三角形是等腰三角形,即1个;
作OA的垂直平分线交x轴于一点P1,
则AP=OP,
此时三角形是等腰三角形,即1个;
2+1+1=4,
当OA与x轴正半轴夹角等于60°的时候,图中的P1,P'和P'会重合,是一个点,加上原来的负半轴的P点,总共2个点,
故答案为4或2.

以A为圆心,以OA为半径画弧交x轴于点P″(O除外),此时三角形是等腰三角形,即1个;
作OA的垂直平分线交x轴于一点P1,
则AP=OP,
此时三角形是等腰三角形,即1个;
2+1+1=4,
当OA与x轴正半轴夹角等于60°的时候,图中的P1,P'和P'会重合,是一个点,加上原来的负半轴的P点,总共2个点,
故答案为4或2.
点评:本题考查了等腰三角形的判定和坐标与图形的性质,主要考查学生的动手操作能力和理解能力,注意不要漏解啊.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
下列多项式中,属于二次三项式的是( )
| A、2a+b+c |
| B、a2b+ab+ab2 |
| C、2x+1-x2 |
| D、a2-2ab+b2-1 |
 如图,直线AB与CD相交于点O,已知∠DOE=75°,∠BOE=35°,求∠AOC,∠AOD的度数.
如图,直线AB与CD相交于点O,已知∠DOE=75°,∠BOE=35°,求∠AOC,∠AOD的度数.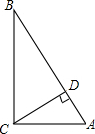 如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AD=
如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AD=