题目内容
10.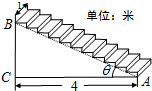 一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )| A. | (4+4sinθ)米2 | B. | $\frac{4}{cosθ}$米2 | C. | (4+$\frac{4}{tanθ}$)米2 | D. | (4+4tanθ)米2 |
分析 由三角函数表示出BC,得出AC+BC的长度,由矩形的面积即可得出结果.
解答 解:在Rt△ABC中,BC=AC•tanθ=4tanθ(米),
∴AC+BC=4+4tanθ(米),
∴地毯的面积至少需要1×(4+4tanθ)=4+4tanθ(米2);
故选:D.
点评 本题考查了解直角三角形的应用、矩形面积的计算;由三角函数表示出BC是解决问题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
20.下列运算正确的是( )
| A. | x3x2=x6 | B. | x2+x2=2x4 | C. | (-2x)2=-4x2 | D. | (-2x3)(-3x2)=6x5 |
1.下列不等式变形正确的是( )
| A. | 如果a>b,那么-3a>-3b | B. | 如果2a>-3,那么$a<-\frac{3}{2}$ | ||
| C. | 如果-a>-b,那么m-a>m-b | D. | 如果$-\frac{1}{2}>-1$,那么$-\frac{1}{2}a>-a$ |
18. 将一副三角板按图中方式叠放,则∠α等于( )
将一副三角板按图中方式叠放,则∠α等于( )
 将一副三角板按图中方式叠放,则∠α等于( )
将一副三角板按图中方式叠放,则∠α等于( )| A. | 90° | B. | 75° | C. | 60° | D. | 45° |
5.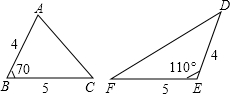 如图,王明同学画了两个不同形状的三角形,并将有关数据在图
如图,王明同学画了两个不同形状的三角形,并将有关数据在图
中进行了标注,两个三角形的面积分别记为S△ABC和S△DEF,则( )
 如图,王明同学画了两个不同形状的三角形,并将有关数据在图
如图,王明同学画了两个不同形状的三角形,并将有关数据在图中进行了标注,两个三角形的面积分别记为S△ABC和S△DEF,则( )
| A. | S△ABC>S△DEF | B. | S△ABC<S△DEF | ||
| C. | S△ABC=S△DEF | D. | 无法确定面积关系 |
15.下列各式中与a-b+c相等的是( )
| A. | a-(+b)-(+c) | B. | a-(+b)-(-c) | C. | a+(-b)+(-c) | D. | a+(-b)-(+c) |
20.下列式子计算结果最大的是( )
| A. | 8×109-2×108 | B. | 8×1010-2×109 | C. | 9×109-2×108 | D. | 9×1010-2×109 |



