题目内容
14.在同一直角坐标系中,函数y=ax+a和y=-ax2+a(a为常数,且a≠0)的图象可以是( )| A. |  | B. |  | C. |  | D. |  |
分析 本题可先由一次函数y=ax+a图象得到a的正负,再与二次函数y=-ax2+a的图象相比较看是否一致.
解答 解:A、由一次函数y=ax+a的图象可得:a<0,此时二次函数y=-ax2+a的图象应该开口向下,对称轴在y轴的负半轴,故选项错误;
B、由一次函数y=ax+a的图象可得:a<0,此时二次函数y=-ax2+a的图象应该开口向下,对称轴在y轴的负半轴,故选项错误;
C、由一次函数y=ax+a的图象可得:a>0,此时二次函数y=-ax2+a的图象应该开口向上,对称轴在y轴的正半轴,故选项错误;
D、由一次函数y=ax+a的图象可得:a<0,此时二次函数y=-ax2+a的图象应该开口向下,对称轴在y轴的负半轴,故选项正确.
故选D.
点评 本本题考查二次函数及一次函数的图象的性质;用到的知识点为:二次函数和一次函数的常数项是图象与y轴交点的纵坐标;一次函数的一次项系数大于0,图象经过一、三象限;小于0,经过二、四象限;二次函数的二次项系数大于0,图象开口向上;二次项系数小于0,图象开口向下.

练习册系列答案
相关题目
14.从长度分别为2,4,6,7的四条线段中随机取三条,能构成三角形的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
9.已知二次函数y=ax2+bx的图象经过点A(-1,1),则ab有( )
| A. | 最大值1 | B. | 最大值2 | C. | 最小值0 | D. | 最小值$-\frac{1}{4}$ |
4.若a,b,c都是负数,并且$\frac{c}{a+b}<\frac{a}{b+c}<\frac{b}{c+a}$,则a、b、c中( )
| A. | a最大 | B. | b最大 | C. | c最大 | D. | c最小 |
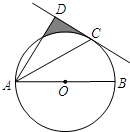 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.若AB=$2\sqrt{6}$,∠BAC=30°,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}$-π.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.若AB=$2\sqrt{6}$,∠BAC=30°,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}$-π.
 如图,在正方形ABCD中,E是CD边上一点(与C、D不重合),DF⊥AE,垂足为G,交BC于F.
如图,在正方形ABCD中,E是CD边上一点(与C、D不重合),DF⊥AE,垂足为G,交BC于F.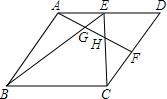 如图,四边形ABCD是平行四边形,E为AD中点,F为CD中点,连接AF、BE、CE,若△EGH的面积为1,则四边形ABCD的面积为30.
如图,四边形ABCD是平行四边形,E为AD中点,F为CD中点,连接AF、BE、CE,若△EGH的面积为1,则四边形ABCD的面积为30.