题目内容
4.若a,b,c都是负数,并且$\frac{c}{a+b}<\frac{a}{b+c}<\frac{b}{c+a}$,则a、b、c中( )| A. | a最大 | B. | b最大 | C. | c最大 | D. | c最小 |
分析 根据不等式的性质,在不等式两边同时加上同一个数,不等号的方向不变和分式的加法法则计算即可.
解答 解:∵$\frac{c}{a+b}<\frac{a}{b+c}<\frac{b}{c+a}$,
∴$\frac{c}{a+b}+1<\frac{a}{b+c}+1<\frac{b}{c+a}+1$,
∴$\frac{a+b+c}{a+b}$<$\frac{a+b+c}{b+c}$<$\frac{a+b+c}{c+a}$,又a、b、c都是负数,
∴a+b<b+c<c+a,
∴b<a<c,
故选:C.
点评 本题考查的是分式的混合运算和不等式的性质,掌握分式的加减运算法则是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
19.在平面直角坐标系中,直线y=kx-k的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
9.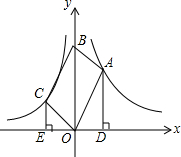 在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
 在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )| A. | 4:9 | B. | 2:3 | C. | 3:2 | D. | 9:4 |
16.已知在函数y=kx+b,其中常数k>0、b<0,那么这个函数的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |




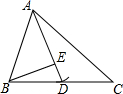 如图,在△ABC中,AC>AB,以点A为圆心、AB长为半径的弧恰交BC于点D,连接AD,过点B作BE⊥AD,垂足为E.
如图,在△ABC中,AC>AB,以点A为圆心、AB长为半径的弧恰交BC于点D,连接AD,过点B作BE⊥AD,垂足为E.