题目内容
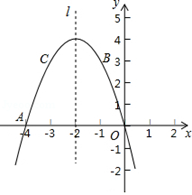
如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数 在第一象限内的图像与△ABC有交点,则
在第一象限内的图像与△ABC有交点,则 的取值范围是
的取值范围是
A.2≤ ≤ ≤ | B.6≤ ≤10 ≤10 | C.2≤ ≤6 ≤6 | D.2≤ ≤ ≤ |
A.
解析试题分析:把A点的坐标代入即可求出k的最小值;当反比例函数和直线BC相交时,求出b2﹣4ac的值,得出k的最大值.
把点A(1,2)代入 得:k=2;
得:k=2;
C的坐标是(6,1),B的坐标是(2,5),
设直线BC的解析式是y=kx+b,
则 ,
,
解得: ,
,
则函数的解析式是: y=﹣x+7,
根据题意,得: =﹣x+7,即x2﹣7x+k=0,
=﹣x+7,即x2﹣7x+k=0,
△=49﹣4k≥0,
解得:k≤ .
.
则k的范围是:2≤k≤ .
.
故选A.
考点:反比例函数综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在平面直角坐标系中,反比例函数y= 的图象的两支分别在( )
的图象的两支分别在( )
| A.第一、三象限 | B.第一、二象限 |
| C.第二、四象限 | D.第三、四象限 |
已知反比例函数 ,下列结论不正确的是
,下列结论不正确的是
| A.图象必经过点(-1,3) |
| B.y随x的增大而增大 |
| C.图象在第二、四象限内 |
| D.若x>1,则y>-3 |
若点(3,4)是反比例函数 图像上一点,则此函数图像必经过点( )
图像上一点,则此函数图像必经过点( )
| A.(3,-4) | B.(2,-6) | C.(4,-3) | D.(2,6) |
 ,EF⊥OD,垂足为F.
,EF⊥OD,垂足为F.
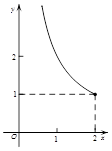
 ,长y宽x的函数,其函数图像大致是
,长y宽x的函数,其函数图像大致是

 B.
B. C.
C. D.
D.



