题目内容
 已知:如图,∠A=∠D=90°,AC=BD.求证:
已知:如图,∠A=∠D=90°,AC=BD.求证:(1)△BAC≌△CDB;
(2)OB=OC.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)直接根据HL就可以得出△BAC≌△CDB;
(2)由△BAC≌△CDB就可以得出∠ACB=∠DBC就可以得出OB=OC.
(2)由△BAC≌△CDB就可以得出∠ACB=∠DBC就可以得出OB=OC.
解答:证明:(1)∵∠A=∠D=90°,
∴△BAC和△CDB都是直角三角形.
在Rt△BAC和Rt△CDB中,
,
∴Rt△BAC≌Rt△CDB(HL);
(2)∵Rt△BAC≌Rt△CDB,
∴∠ACB=∠DBC,
∴OB=OC.
∴△BAC和△CDB都是直角三角形.
在Rt△BAC和Rt△CDB中,
|
∴Rt△BAC≌Rt△CDB(HL);
(2)∵Rt△BAC≌Rt△CDB,
∴∠ACB=∠DBC,
∴OB=OC.
点评:本题考查了HL证明三角形全等的判定及性质的运用,等腰三角形的判定的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 如图,两条相交直线l1与l2的夹角是45°,都是一个图案的对称轴,画出这个图案的其余部分.这个图案共有多少条对称轴?
如图,两条相交直线l1与l2的夹角是45°,都是一个图案的对称轴,画出这个图案的其余部分.这个图案共有多少条对称轴? 如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:
如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证: 如图,点P的坐标为(4,0),⊙P的半径为5,且⊙P与x轴交于点A,B,与y轴交于点C,D,试求出点A,B,C,D的坐标.
如图,点P的坐标为(4,0),⊙P的半径为5,且⊙P与x轴交于点A,B,与y轴交于点C,D,试求出点A,B,C,D的坐标. 如图所示,有两个村庄A和B被一条河隔开,现要架一座桥(桥与河岸垂直),使A和B之间路程最短,请你设计一种方案.
如图所示,有两个村庄A和B被一条河隔开,现要架一座桥(桥与河岸垂直),使A和B之间路程最短,请你设计一种方案.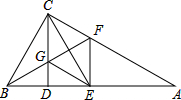 如图,在△ABC中,∠ACB=90°,BF平分∠ABC,CD⊥AB于点D,与BF交于点G,GE∥AC.求证:CE与FG互相垂直平分.
如图,在△ABC中,∠ACB=90°,BF平分∠ABC,CD⊥AB于点D,与BF交于点G,GE∥AC.求证:CE与FG互相垂直平分. 如图,在△ABC中,∠ABC的平分线交AC于点D,DE∥BC.求证:△EBD是等腰三角形.
如图,在△ABC中,∠ABC的平分线交AC于点D,DE∥BC.求证:△EBD是等腰三角形.