题目内容
下列一元二次方程中,没有实数根的是( )
| A、x+2x-1=0 | ||
B、x+2
| ||
C、x+
| ||
| D、-x+2x+2=0 |
考点:根的判别式
专题:
分析:根据一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根分别对每一项进行分析判断即可.
解答:解:A.∵x+2x-1=0中△=b2-4ac=22-4×1×(-1)=8>0,∴它有两个不相等的实数根;
B.∵x+2
x-1=0中△=b2-4ac═(2
)2-4×1×(-1)=12>0,∴它有两个不相等的实数根;
C.∵x2+
x+1=0中△=b2-4ac=(
)2-4×1×1=-2<0,∴它没有实数根;
D.∵-x2+2x+2=0中△=b2-4ac=22-4×(-1)×2=12>0,∴它有两个不等的实数根,
故选C.
B.∵x+2
| 2 |
| 2 |
C.∵x2+
| 2 |
| 2 |
D.∵-x2+2x+2=0中△=b2-4ac=22-4×(-1)×2=12>0,∴它有两个不等的实数根,
故选C.
点评:此题考查了一元二次方程根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
下列二次根式,不能与
合并的是( )
| 12 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
多项式9a2-4b2分解因式的结果是( )
| A、(3a+2b)(3a-2b) |
| B、(3a-2b)2 |
| C、(9a+4b)(9a-4b) |
| D、(2a+3b)(2a-3b) |
下列各组图形中,AD是△ABC的高的图形是( )
A、 |
B、 |
C、 |
D、 |
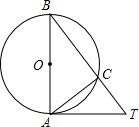 如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )
如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )| A、AB=4,AT=3,BT=5 |
| B、∠B=45°,AB=AT |
| C、∠B=55°,∠TAC=55° |
| D、∠ATC=∠B |
若抛物线y=0.5x2+3x+m与x轴没有交点,则m的取值范围是( )
| A、m≤4.5 |
| B、m≥4.5 |
| C、m>4.5 |
| D、以上都不对 |
上海世博会累计入园参观人数约为7300万人次,该数用科学记数法可以表示为( )
| A、7.3×108人次 |
| B、7.3×107人次 |
| C、7.3×106人次 |
| D、7.3×105人次 |