题目内容
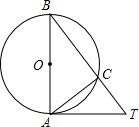 如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )
如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )| A、AB=4,AT=3,BT=5 |
| B、∠B=45°,AB=AT |
| C、∠B=55°,∠TAC=55° |
| D、∠ATC=∠B |
考点:切线的判定
专题:
分析:分别利用切线的判定进而得出得出∠BAT=90°,得出答案即可.
解答:解:A、∵AB=4,AT=3,BT=5,
∴AB2+AT2=BT2,
∴△BAT是直角三角形,
∴∠BAT=90°,
∴直线AT是⊙O的切线,故此选项错误;
B、∵∠B=45°,AB=AT,
∴∠T=45°,
∴∠BAT=90°,
∴直线AT是⊙O的切线,故此选项错误;
C、∵AB为直径,
∴∠BAC=90°,
∵∠B=55°,
∴∠BAC=35°,
∵∠TAC=55°,
∴∠CAT=90°,
∴直线AT是⊙O的切线,故此选项错误;
D、∠ATC=∠B,无法得出直线AT是⊙O的切线,故此选项正确.
故选:D.
∴AB2+AT2=BT2,
∴△BAT是直角三角形,
∴∠BAT=90°,
∴直线AT是⊙O的切线,故此选项错误;

B、∵∠B=45°,AB=AT,
∴∠T=45°,
∴∠BAT=90°,
∴直线AT是⊙O的切线,故此选项错误;
C、∵AB为直径,
∴∠BAC=90°,
∵∠B=55°,
∴∠BAC=35°,
∵∠TAC=55°,
∴∠CAT=90°,
∴直线AT是⊙O的切线,故此选项错误;
D、∠ATC=∠B,无法得出直线AT是⊙O的切线,故此选项正确.
故选:D.
点评:此题主要考查了切线的判定,正确把握判定方法得出∠BAT=90°是解题关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
若|-a|=2,则a的值是( )
| A、-2 | B、2 | C、±2 | D、都不是 |
下列式子中,-3x,
,
,
,
,
中,分式的个数是( )
| x+y |
| x-y |
| x2y-xy2 |
| 3 |
| 5+y |
| π |
| 3 |
| x |
| x |
| 4x2y |
| A、1 | B、2 | C、3 | D、4 |
下列一元二次方程中,没有实数根的是( )
| A、x+2x-1=0 | ||
B、x+2
| ||
C、x+
| ||
| D、-x+2x+2=0 |
分式方程
-
=0的解为( )
| 3 |
| x |
| 2 |
| x-2 |
| A、x=6 | B、x=-6 |
| C、x=2 | D、原方程无解 |
若分式
有意义,则x的取值范围是( )
| x-2 |
| x+1 |
| A、x≠-1 | B、x≠2 |
| C、x≠-2 | D、x=-1 |
下列说法正确的是( )
| A、平行四边形的对角互补,邻角相等 |
| B、对角线相等的四边形是矩形 |
| C、一组对边平行且一组对角相等的四边形是平行四边形 |
| D、平行四边形是轴对称图形 |