题目内容
若抛物线y=0.5x2+3x+m与x轴没有交点,则m的取值范围是( )
| A、m≤4.5 |
| B、m≥4.5 |
| C、m>4.5 |
| D、以上都不对 |
考点:抛物线与x轴的交点
专题:
分析:若二次函数y=0.5x2+3x+m的图象与x轴没有交点,则一元二次方程0=y=0.5x2+3x+m的判别式小于0,从而求得m的取值范围.
解答:解:∵二次函数y=0.5x2+3x+m的图象与x轴没有交点,
∴令y=0时,0.5x2+3x+m=0的判别式△<0,
即b2-4ac=9-2m<0,
解得m>4.5,
故选C.
∴令y=0时,0.5x2+3x+m=0的判别式△<0,
即b2-4ac=9-2m<0,
解得m>4.5,
故选C.
点评:本题考查了抛物线与x轴的交点问题,注:当抛物线y=ax2+bx+c与轴有两个交点时,一元二次方程ax2+bx+c=0有两个不等的实数根即△>0;当抛物线y=ax2+bx+c与轴有一个交点时,一元二次方程ax2+bx+c=0有两个相等的实数根即△=0;当抛物线y=ax2+bx+c与轴无交点时,一元二次方程ax2+bx+c=0无实数根即△<0.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
下面是小强用三根火柴组成的图形,其中符合三角形概念的是( )
A、 |
B、 |
C、 |
D、 |
下列一元二次方程中,没有实数根的是( )
| A、x+2x-1=0 | ||
B、x+2
| ||
C、x+
| ||
| D、-x+2x+2=0 |
下列图案是轴对称图形的有( )个.


| A、1 | B、2 | C、3 | D、4 |
若分式
有意义,则x的取值范围是( )
| x-2 |
| x+1 |
| A、x≠-1 | B、x≠2 |
| C、x≠-2 | D、x=-1 |
下列各式中计算正确的是( )
A、(
| ||
| B、a2•a3=a6 | ||
| C、(-3a-3)2=9a6 | ||
| D、a5+a3=a8 |
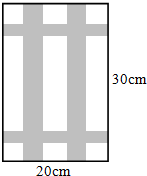 如图,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使所有彩条所占面积为原矩形面积的三分之一,设每个横彩条的宽为2x,则下列方程正确的是( )
如图,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使所有彩条所占面积为原矩形面积的三分之一,设每个横彩条的宽为2x,则下列方程正确的是( )A、(20-3x)(30-2x)=(1-
| ||
B、(20-6x)(30-4x)=
| ||
C、(20-6x)(30-4x)=(1-
| ||
D、(20-2x)(20-3x)=(1-
|