题目内容
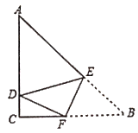
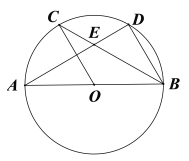
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,DE⊥AC,垂足为E,CF∥AB交AD延长线于点F,连接BF交⊙O于点G,连接DG.
(1)求证:DE为⊙O的切线;
(2)求证:四边形ABFC为菱形;
(3)若OA=5,DG=2![]() ,求线段GF的长.
,求线段GF的长.
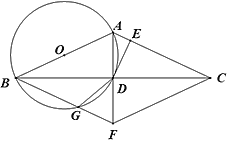
【答案】(1)见解析;(2)见解析;(3)4.
【解析】
(1)如图,连接OD,由等腰三角形的性质可得∠OBD=∠ODB,∠ABC=∠ACB,可证明∠ODB=∠ACB,可得OD//AC,根据DE⊥AC可得DE⊥AC,即可证明DE为⊙O的切线;
(2)由OD//AC,OA=OB可得BD=CD,根据平行线的性质可得∠BAD=∠CFD,∠ABD=∠FCD,利用AAS可证明△ABD≌△FCD,可得AB=CF,可证明四边形ABFC是平行四边形,由AB=AC即可证明四边形ABCF是菱形;
(3)根据圆内接四边形的性质及平角的定义可得∠GDF=∠ABG,∠DGF=∠BAD,可证明△FGD∽△FAB,根据菱形的性质可得∠BAD=∠BFD,即可证明∠DGF=∠BFD,可得DG=DF,利用相似三角形的性质即可求出GF的长.
(1)连接OD,
∵OB=OD,
∴∠OBD=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE为⊙O的切线.
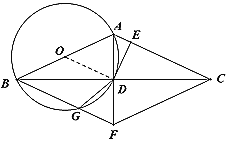
(2)由(1)得,OD∥AC,
又∵OA=OB,
∴DB=DC,
∵CF∥AB,
∴∠BAD=∠CFD,∠ABD=∠FCD,
在△ABD和△ECD中,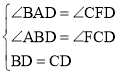 ,
,
∴△ABD≌△FCD,
∴AB=CF,
∴四边形ABFC为平行四边形,
∵AB=AC,
∴平行四边形ABFC为菱形.
(3)∵四边形ABGD内接于⊙O,
∴∠ABG+∠ADG=180°,∠BAD+∠BGD=180°,
∵∠GDF+∠ADG=180°,∠DGF+∠BGD=180°,
∴∠GDF=∠ABG,∠DGF=∠BAD,
∴△FGD∽△FAB,
∴![]() ,
,
∵AB为⊙O的直径,OA=5,
∴AB=10,
∵四边形ABFC为菱形,
∴∠BAD=∠BFD,AF=2DF,
∴∠DGF=∠BFD,
∴DF=DG=2![]() ,
,
∴AF=2DF![]() ,
,
∴![]() .
.

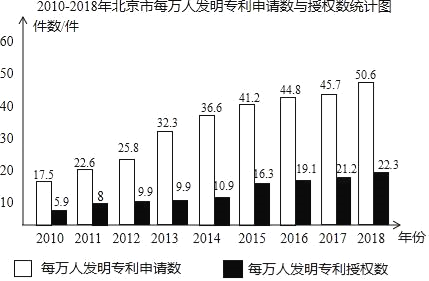
【题目】一辆汽车油箱中有汽油![]() .如果不再加油,那么油箱中的油量
.如果不再加油,那么油箱中的油量![]() (单位:
(单位:![]() )随行驶路程
)随行驶路程![]() (单位:
(单位:![]() )的增加而减少.已知该汽车平均耗油量为
)的增加而减少.已知该汽车平均耗油量为![]() .
.
(Ⅰ)计算并填写下表:
| 10 | 100 | 300 | … |
| … |
(Ⅱ)写出表示![]() 与
与![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,
,![]() 两地的路程约有
两地的路程约有![]() ,当油箱中油量少于
,当油箱中油量少于![]() 时,汽车会自动报警,则这辆汽车在由
时,汽车会自动报警,则这辆汽车在由![]() 地到
地到![]() 地,再由
地,再由![]() 地返回
地返回![]() 地的往返途中,汽车是否会报警?请说明理由.
地的往返途中,汽车是否会报警?请说明理由.