题目内容
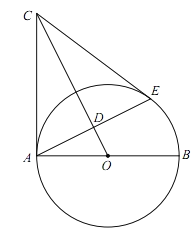
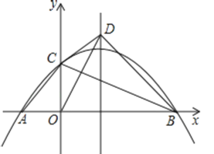
【题目】如图,四边形![]() 内接于半圆
内接于半圆![]() ,
,![]() 为直径,
为直径,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点F.若
于点F.若![]() ,
,![]() ,则
,则![]() 的长为 ( )
的长为 ( )
A.8B.10C.15D.24
【答案】D
【解析】
连接BD,如图,先利用圆周角定理证明∠ADE=∠DAC得到FD=FA=5,再根据余弦的定义计算出AE=3,则EF=4,DE=9,接着证明ΔADEΔDBE,利用相似比得到BE=27,所以AB=30,然后在RtΔABC中利用余弦定义计算出BC=24的长.
连接BD,如图,
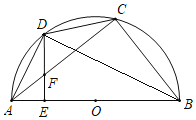
∵AB为直径,
∴∠ADB=∠ACB=90°,
∵AD=CD,
∴∠DAC=∠DCA,
而∠DCA=∠ABD,
∴∠DAC=∠ABD,
∵DE⊥AB,
∴∠ABD+∠BDE=90°,
而∠ADE+∠BDE=90°,
∴∠ABD=∠ADE,
∴∠ADE=∠DAC,
∴FD=FA=5,
在RtΔAEF中,∵cos∠CAB=![]() =
=![]() ,
,
∴AE=3,
∴EF=![]() =4,DE=5+4=9,
=4,DE=5+4=9,
∵∠ADE=∠DBE,∠AED=∠BED,
∴ΔADEΔDBE,
∴DE:BE=AE:DE,即9:BE=3:9,
∴BE=27,
∴AB=3+27=30,
在RtΔABC中,∵cos∠CAB=![]() =
=![]() ,
,
∴AC=30×![]() =18,
=18,
BC=![]() =
=![]() =24,
=24,
故选D.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目