题目内容
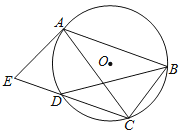
【题目】已知直线y=2x+b与反比例函数y=![]() 的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E,
的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E,
(1)若k=8,且点A的横坐标为1,求b的值;
(2)已知△BEC的面积为4,则k的值为多少?
(3)若将直线旋转,k=8,点E为△ABC的重心且OE=2,求直线AC的解析式.
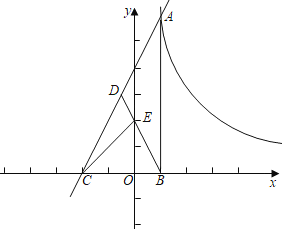
【答案】(1)b=6;(2)k=8;(3)直线AC的解析式为y=2x+4.
【解析】
(1)求出点A的坐标,利用待定系数法即可解决问题.
(2)设A(m,![]() ),则B(m,0),构建一次函数求出点E,点C的坐标(用m,k表示),再利用三角形的面积,构建方程求出k即可.
),则B(m,0),构建一次函数求出点E,点C的坐标(用m,k表示),再利用三角形的面积,构建方程求出k即可.
(3)连接AE,延长AE交BC于J.求出点J的坐标,再根据中点坐标公式构建方程求出k即可解决问题.
解:(1)由题意,A(1,8),
把A(1,8)代入y=2x+b得到b=6.
(2)设A(m,![]() ),则B(m,0),
),则B(m,0),
把A(m,![]() )代入y=2x+b得到b=
)代入y=2x+b得到b=![]() ﹣2m,
﹣2m,
∴直线AC的解析式为y=2x+![]() ﹣2m,
﹣2m,
令y=0,得到x=m﹣![]() ,
,
∴C(m﹣![]() ,0),
,0),
∵AD=DC,
∴D(m﹣![]() ,
,![]() ),
),
设直线BD的解析式为y=k′x+b′,
则有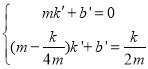 ,
,
解得![]() ,
,
∴直线BD的解析式为y=﹣2x+2m,
∴E(0,2m),
∴OE=2m,BC=OC+OB=![]()
∵S△ECB=4,
∴![]() BCEO=4,
BCEO=4,
∴![]() ×
×![]() ×2m=4,
×2m=4,
∴k=8.
(3)连接AE,延长AE交BC于J.
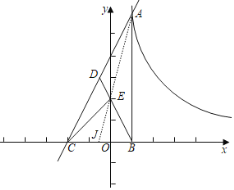
由(2)可知,E(0,2m),
∵OE=2,
∴2m=2,
∴m=1,
∴C((1﹣![]() ,0),B(1,0),A(1,k),
,0),B(1,0),A(1,k),
∴直线AE的解析式为:y=(k﹣2)x+2,
令y=0,得到x=![]() ,
,
∴J(![]() ,0),
,0),
∵E是△ABC的重心,
∴CJ=JB,
∴![]() =
=![]() (1+1﹣
(1+1﹣![]() ),
),
解得k=6或0(舍弃),
∴直线AC的解析式为y=2x+4.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目