题目内容
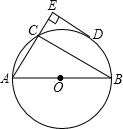 如图,已知AB、AC分别是⊙O的直径和弦,D为
如图,已知AB、AC分别是⊙O的直径和弦,D为 |
| BC |
| A、DE是⊙O的切线 |
| B、直径AB长为20cm |
| C、弦AC长为16cm |
| D、C为弧AD的三等分点 |
考点:切线的判定
专题:
分析:AB是圆的直径,则∠ACB=90°,根据DE垂直于AC的延长线于E,可以证得ED∥BC,则DE⊥OD,即可证得DE是圆的切线,根据切割线定理即可求得AC的长,连接OD,交BC与点F,则四边形DECF是矩形,根据垂径定理即可求得半径.
解答: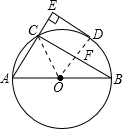 解:连接OD,OC.
解:连接OD,OC.
∵D是弧BC的中点,则OD⊥BC,
∴DE是圆的切线.故A正确;
∴DE2=CE•AE
即36=2AE
∴AE=18,则AC=AE-CE=18-2=16cm.故C正确;
∵AB是圆的直径.
∴∠ACB=90°,
∵DE垂直于AC的延长线于E.
D是弧BC的中点,则OD⊥BC,
∴四边形CFDE是矩形.
∴CF=DE=6cm.BC=2CF=12cm.
在直角△ABC中,根据勾股定理可得:AB=
=
=20cm.故B正确;
在直角△ABC中,AC=16,AB=20,
则∠ABC≠30°,
而D是弧BC的中点.
∴弧AC≠弧CD.故D错误;
故选D.
 解:连接OD,OC.
解:连接OD,OC.∵D是弧BC的中点,则OD⊥BC,
∴DE是圆的切线.故A正确;
∴DE2=CE•AE
即36=2AE
∴AE=18,则AC=AE-CE=18-2=16cm.故C正确;
∵AB是圆的直径.
∴∠ACB=90°,
∵DE垂直于AC的延长线于E.
D是弧BC的中点,则OD⊥BC,
∴四边形CFDE是矩形.
∴CF=DE=6cm.BC=2CF=12cm.
在直角△ABC中,根据勾股定理可得:AB=
| AC2+BC2 |
| 162+122 |
在直角△ABC中,AC=16,AB=20,
则∠ABC≠30°,
而D是弧BC的中点.
∴弧AC≠弧CD.故D错误;
故选D.
点评:本题主要考查了垂径定理,以及切割线定理,利用垂径定理可以把圆的弦、半径的计算转化为解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a,b,c是三角形的三边长,如果满足(a-b)2+
+|c2-64|=0,则三角形的形状是( )
| b-8 |
| A、底和腰不相等的等腰三角形 |
| B、等边三角形 |
| C、钝角三角形 |
| D、直角三角形 |
如图,y是x的函数图象的是( )
A、 |
B、 |
C、 |
D、 |
下列条件中能组成三角形的是( )
| A、7cm,7cm,12cm |
| B、5cm,3cm,9cm |
| C、6cm,9cm,16cm |
| D、5cm,6cm,11cm |
下列各数组中,能作为直角三角形三边长的是( )
| A、1,1,2 |
| B、2,3,4 |
| C、2,3,5 |
| D、3,4,5 |
对于反比例函数y=
(k<0),下列说法正确的是( )
| k |
| x |
| A、图象经过点(1,-k) |
| B、图象位于第一、三象限 |
| C、图象是中心对称图形 |
| D、当x<0时,y随x的增大而减小 |
下列方程无实数根的是( )
| A、x2=0 |
| B、x2-1=0 |
| C、x2+1=0 |
| D、x2-x=0 |