题目内容
8.某市对一段全长2000米的道路进行改造,为了尽量减少施工对城市交通所造成的影响,实际施工时,若每天修路比原来计划提高效率25%,就可以提前5天完成修路任务.(1)求修这段路计划用多少天?
(2)有甲、乙两个工程队参与修路施工,其中甲队每天可修路120米,乙队每天可修路80米,若每天只安排一个工程队施工,在保证至少提前5天完成修路任务的前提下,甲工程队至少要修路多少天?
分析 (1)设原计划每天修x米,根据原计划的工作时间-实际的工作时间=5,然后列出方程可求出结果,进一步代入得出答案即可;
(2)设甲工程队至少要修路a天,则乙工程队要修路20-a天,根据工作总量的和不小于2000列出不等式解决问题即可.
解答 解:(1)设原计划每天修x米,由题意得
$\frac{2000}{x}$-$\frac{2000}{x(1+25%)}$=5
解得x=80,
经检验x=80是原方程的解,
则$\frac{2000}{x}$=25天
答:修这段路计划用20天,.
(2)设甲工程队至少要修路a天,则乙工程队要修路20-a天,根据题意得
120a+80(20-a)≥2000
解得a≥10
所以a最小等于10.
答:甲工程队至少要修路10天.
点评 此题考查分式方程的应用,一元一次不等式的运用,找出题目蕴含的数量关系是解决问题的关键.

练习册系列答案
相关题目
19.方程2x2+3x+2=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有两个实数根 | D. | 沒有实数根 |
16.一元二次方程x2+4x+4=0的根是( )
| A. | x1=4,x2=-4 | B. | x1=x2=-2 | C. | x1=2,x2=-2 | D. | x1=0,x2=-2 |
20.在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
| A. | 11+$\frac{11\sqrt{3}}{2}$ | B. | 11+$\frac{11\sqrt{3}}{2}$或1+$\frac{\sqrt{3}}{2}$ | ||
| C. | 11+$\frac{11\sqrt{3}}{2}$或11-$\frac{11\sqrt{3}}{2}$ | D. | 11-$\frac{11\sqrt{3}}{2}$ |
17.下列说法正确的是( )
| A. | $\sqrt{9}$的算术平方根是$\sqrt{3}$ | B. | ±$\frac{3}{4}$是$\frac{9}{16}$的算术平方根 | ||
| C. | -8的立方根是2 | D. | 0没有平方根 |
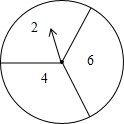 把一个转盘平均分成三等份,依次标上数字2、4、6,小红自由转动转盘两次,把第一次转动停止后指针指向的数字记作x,把第二次转动停止后指针指向的数字除以2所得的商记作y,以x,y,5的边长的三条线段,能够构成三角形的概率为$\frac{4}{9}$.
把一个转盘平均分成三等份,依次标上数字2、4、6,小红自由转动转盘两次,把第一次转动停止后指针指向的数字记作x,把第二次转动停止后指针指向的数字除以2所得的商记作y,以x,y,5的边长的三条线段,能够构成三角形的概率为$\frac{4}{9}$. 如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n=2时,四边形ABEC是矩形.
如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n=2时,四边形ABEC是矩形.