题目内容
5.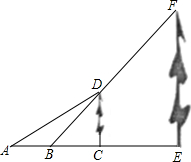 如图所示,小明家小区空地上有两棵笔直的树CD、EF.一天,他在A处测得树顶D的仰角∠DAC=30°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A、B、C、E四点在一条直线上,求树EF的高度.($\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4,结果保留一位小数)
如图所示,小明家小区空地上有两棵笔直的树CD、EF.一天,他在A处测得树顶D的仰角∠DAC=30°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A、B、C、E四点在一条直线上,求树EF的高度.($\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4,结果保留一位小数)
分析 设CD=xm,先在Rt△BCD中,由于∠DBC=45°,则根据等腰直角三角形的性质得BC=CD=x,再在Rt△DAC中,利用正切定义得到x+2=$\sqrt{3}$x,解得x=$\sqrt{3}$+1,即BC=CD=$\sqrt{3}$+1,然后在Rt△FBE中根据等腰直角三角形的性质得FE=BE=BC+CE≈5.7.
解答 解:设CD=xm,
在Rt△BCD中,∵∠DBC=45°,
∴BC=CD=x,
在Rt△DAC中,∵∠DAC=30°,
∴tan∠DAC=$\frac{CD}{AC}$,
∴x+2=$\sqrt{3}$x,解得x=$\sqrt{3}$+1,
∴BC=CD=$\sqrt{3}$+1,
在Rt△FBE中,∵∠DBC=45°,
∴FE=BE=BC+CE=$\sqrt{3}$+1+3≈5.7.
答:树EF的高度约为5.7m.
点评 本题考查了解直角三角形的应用-仰角俯角问题:仰角是向上看的视线与水平线的夹角;俯角是向下看的视线与水平线的夹角.解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
13.甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为S甲2=17、S乙2=25,下列说法正确的是( )
| 第一次 | 第二次 | 第三次 | 第四次 | |
| 甲 | 87 | 95 | 85 | 93 |
| 乙 | 80 | 80 | 90 | 90 |
| A. | 甲同学四次数学测试成绩的平均数是89分 | |
| B. | 甲同学四次数学测试成绩的中位数是90分 | |
| C. | 乙同学四次数学测试成绩的众数是80分 | |
| D. | 乙同学四次数学测试成绩较稳定 |
10.分解因式2x2-4x+2的最终结果是( )
| A. | 2x(x-2) | B. | 2(x-1)2 | C. | 2(x2-2x+1) | D. | (2x-2)2 |
14.下列图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图所示,要用防护网围成长方形花坛,其中一面利用现有的一段墙,且在与墙平行的一边开一个2米宽的门.现有防护网的长度为91米,花坛的面积需要1081平方米,若墙长50米,求花坛的长和宽.
如图所示,要用防护网围成长方形花坛,其中一面利用现有的一段墙,且在与墙平行的一边开一个2米宽的门.现有防护网的长度为91米,花坛的面积需要1081平方米,若墙长50米,求花坛的长和宽.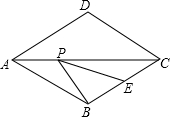 如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为$\sqrt{3}$+1.
如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为$\sqrt{3}$+1.