题目内容
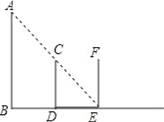
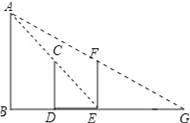
如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长.

【考点】相似三角形的应用.
【分析】画出图形,根据题意得出BD=CD=DE=EF=1.6米,AB∥CD,得出BE=3.2米,△CDE∽△ABE,由相似三角形的性质得出比例式求出AB,同理:△FEG∽△ABG,得出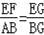
 ,即可得出EG的长.
,即可得出EG的长.
【解答】解:如图所示:
线段EG表示小明此时的影子;
根据题意得:BD=CD=DE=EF=1.6米,AB∥CD,
∴BE=3.2米,△CDE∽△ABE,
∴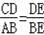
 ,即
,即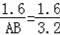
 ,
,
解得:AB=3.2米,
同理:△FEG∽△ABG,
∴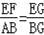
 ,即
,即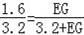
 ,
,
解得:EG=3.2米;
答:此时小明的影长为3.2米.

【点评】本题考查了相似三角形的应用、相似三角形的判定与性质;证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 ,其中
,其中 ,
, .
.


 (x>0) B.y=
(x>0) B.y=
 (x>0) C.y=
(x>0) C.y=