题目内容
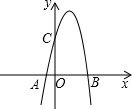 如图,已知二次函数的图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
如图,已知二次函数的图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.(1)求点C的坐标;
(2)求二次函数的解析式,并化成一般形式.
考点:待定系数法求二次函数解析式
专题:
分析:(1)根据题目所给的信息可以知道OC=AB=5,点C在y轴上可以写出点C的坐标;
(2)二次函数图象经过点A、B、C;这三个点的坐标已知,根据三点法确定这一二次函数解析式.
(2)二次函数图象经过点A、B、C;这三个点的坐标已知,根据三点法确定这一二次函数解析式.
解答:解:(1)∵点A的坐标为(-1,0),点B的坐标为(4,0),
∴OC=AB=5,
∴点C的坐标为(0,5);
(2)设二次函数解析式为:y=ax2+bx+5,
把A(-1,0)、B(4,0)代入原函数解析式得出:
a=-
,b=
;
所以这个二次函数的解析式为:y=-
x2+
x+5.
∴OC=AB=5,
∴点C的坐标为(0,5);
(2)设二次函数解析式为:y=ax2+bx+5,
把A(-1,0)、B(4,0)代入原函数解析式得出:
a=-
| 5 |
| 4 |
| 15 |
| 4 |
所以这个二次函数的解析式为:y=-
| 5 |
| 4 |
| 15 |
| 4 |
点评:此题主要考查了待定系数法求二次函数解析式,同时还考查了方程组的解法等知识.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
在同一平面直角坐标系中,将函数y=2x2+4x+1的图象沿x轴方向向右平移2个单位后再沿y轴向下平移1个单位,得到图象的顶点坐标是( )
| A、(-1,1) |
| B、(1,-2) |
| C、(2,-2) |
| D、(1,-2) |
一个扇形的圆心角为120°,半径为3,则这个扇形的面积为( )
| A、3π | B、9π | C、2π | D、4π |
 如图所示,已知菱形OABC,点C在x轴正半轴上,直线y=x经过一象限内点A,菱形OABC的面积等于
如图所示,已知菱形OABC,点C在x轴正半轴上,直线y=x经过一象限内点A,菱形OABC的面积等于 如图,有一个转盘被分成6个相同的扇形区域,颜色分别为红、黄、绿、白四中颜色,指针的位置固定,转动转盘后任其自由停止,如果指针指在等分线上,那么重新转动,直至指针指向某个扇形区域内为止,请你完成以下问题:
如图,有一个转盘被分成6个相同的扇形区域,颜色分别为红、黄、绿、白四中颜色,指针的位置固定,转动转盘后任其自由停止,如果指针指在等分线上,那么重新转动,直至指针指向某个扇形区域内为止,请你完成以下问题: 如图,水库大坝的横截面是梯形,坝顶AD宽5米,坝高10米,斜坡CD的坡角为45°,斜坡AB的坡度i=1:1.5,那么坝底BC的长度为
如图,水库大坝的横截面是梯形,坝顶AD宽5米,坝高10米,斜坡CD的坡角为45°,斜坡AB的坡度i=1:1.5,那么坝底BC的长度为