题目内容
14．
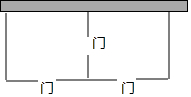某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（不包括门）总长为27m，求饲养室占地的最大面积是多少？
分析 设垂直于墙的边长为xm，则平行于墙的一边长为27+3-3x，根据矩形面积公式可得S=x（27+3-3x）=-3x2+30x，由二次函数性质可得答案．
解答 解：设垂直于墙的边长为xm．
由题意可得面积S=x（27+3-3x）
=x（30-3x）
=-3x2+30x
∴-$\frac{b}{2a}$=-$\frac{30}{2×（-3）}$=5，
当x=5时，S最大=5（30-3×5）=75
答：饲养室占地的最大面积是75m2．
点评 本题主要考查二次函数的应用，根据题意得出平行于墙的一边长及熟练掌握二次函数性质是关键．
练习册系列答案
备战中考寒假系列答案
相关题目
2．某校举办初中生演讲比赛，每班派两名学生参赛，现某班有A、B、C三名学生竞选，他们的笔试成绩和口试成绩（单位：分）分别用两种方式进行了统计，如表和图（1）：
（1）m=90，并将图（1）补充完整；
（2）竞选的最后一个程序是由本校的300名学生代表进行投票，每票计1分，三名候选人的得分情况如图（2）（没有弃权票，每名学生只能推荐一人）；
①若将笔试、口试、得票三项测试得分按4：3：3的比例确定最后成绩，请计算学生A的最后成绩；
②若A、B、C三名学生中有一名男生，两名女生，选其中两名学生参赛，求恰好选中一男一女的概率．（要求用树状图或列表法写出分析过程）
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | m | 80 | 85 |
（1）m=90，并将图（1）补充完整；
（2）竞选的最后一个程序是由本校的300名学生代表进行投票，每票计1分，三名候选人的得分情况如图（2）（没有弃权票，每名学生只能推荐一人）；
①若将笔试、口试、得票三项测试得分按4：3：3的比例确定最后成绩，请计算学生A的最后成绩；
②若A、B、C三名学生中有一名男生，两名女生，选其中两名学生参赛，求恰好选中一男一女的概率．（要求用树状图或列表法写出分析过程）
如图：已知在Rt△ABC中，∠ACB=90°，∠BAC=36°，在直线AC上找点P，使△ABP是等腰三角形，则∠APB的度数为72°或18°或108°或36°．