题目内容
 如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,求证:△AFC是等腰三角形.
如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,求证:△AFC是等腰三角形.考点:等腰三角形的判定
专题:证明题
分析:根据AAS推出△ABD≌△CBE,根据全等三角形的性质得出AB=BC,求出AE=CD,根据AAS推出△AEF≌△CDF即可.
解答:证明:∵在△ABD和△CBE中,
,
∴△ABD≌△CBE(AAS),
∴AB=BC,
∵BE=BD,
∴AE=CD,
在△AEF和△CDF中,
∴△AEF≌△CDF(AAS),
∴AF=CF,
∴△AFC是等腰三角形.
|
∴△ABD≌△CBE(AAS),
∴AB=BC,
∵BE=BD,
∴AE=CD,
在△AEF和△CDF中,
|
∴△AEF≌△CDF(AAS),
∴AF=CF,
∴△AFC是等腰三角形.
点评:本题考查了全等三角形的性质和判定,等腰三角形的判定的应用,能求出AF=CF是解此题的关键,注意:有两边相等的三角形是等腰三角形.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 如图,E为等边△ABC的边AC上一点,且∠1=∠2,CD=BE,试判定△ADE的形状,并说明理由.
如图,E为等边△ABC的边AC上一点,且∠1=∠2,CD=BE,试判定△ADE的形状,并说明理由. 如图,AB=DE,AC=DF,BE=CF,且B,E,C,F在同一条直线上,若∠EGC=80°,求∠A的度数.
如图,AB=DE,AC=DF,BE=CF,且B,E,C,F在同一条直线上,若∠EGC=80°,求∠A的度数.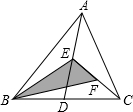 如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE中点,且S△ABC=4平方厘米,则S△BEF的值为
如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE中点,且S△ABC=4平方厘米,则S△BEF的值为 如图,DE分别是AB,AC上一点,AB•AD=AC•AE,△AED与△ABC相似吗?为什么?
如图,DE分别是AB,AC上一点,AB•AD=AC•AE,△AED与△ABC相似吗?为什么?