题目内容
17.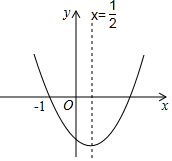 抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的两根是( )
抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的两根是( )| A. | x1=-1,x2=$\frac{1}{2}$ | B. | x1=-1,x2=0 | C. | x1=-1,x2=2 | D. | x1=-1,x2=$\frac{3}{2}$ |
分析 首先计算出抛物线与x轴的另一交点,关于x的方程ax2+bx+c=0的根就是函数线y=ax2+bx+c(a≠0)的图象与x轴的交点的横坐标,据此即可求解.
解答 解:∵抛物线y=ax2+bx+c与x轴交于(-1,0),对称轴是x=$\frac{1}{2}$,
∴抛物线与x轴的另一交点是(2,0),
∴一元二次方程ax2+bx+c=0的两根是x1=-1,x2=2,
故选:C.
点评 本题考查了抛物线与x轴的交点,理解方程ax2+bx+c=0的根就是函数线y=ax2+bx+c(a≠0)的图象与x轴的交点的横坐标是关键.

练习册系列答案
相关题目
5.计算-2-8的结果是( )
| A. | -6 | B. | -10 | C. | 10 | D. | 6 |
12.下列图案中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.某商场2012年的销售利润为a,预计以后每年比上一年增长b%,那么2013年该商场的销售总利润将是( )
| A. | a(1+b) | B. | a(1+b%) | C. | a+a(b%) | D. | a+ab |
6.已知,等腰三角形的两边长是5厘米和11厘米,它的周长是( )
| A. | 21厘米 | B. | 27厘米 | C. | 21厘米或27厘米 | D. | 16厘米 |
7.如果ab=1,则( )
| A. | a、b互为相反数 | B. | |a|=|b| | ||
| C. | a、b互为倒数 | D. | a、b中至少有一个为1 |
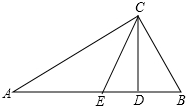 如图,Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,CD是斜边AB上的高,CE是中线,DE=2.
如图,Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,CD是斜边AB上的高,CE是中线,DE=2.