题目内容
14.a、b、c为△ABC的三边,当m>0时,关于x的方程c(x2+m)+b(x2-m)-2$\sqrt{m}$ax=0有两个相等的实数根.(1)将方程整理为关于x的一元二次方程的一般形式;
(2)求证:△ABC为直角三角形.
分析 (1)把方程整理成一般式得(c+b)x2-2$\sqrt{m}$ax+m(c-b)=0;
(2)根据根的判别式得出(-2$\sqrt{m}$a)2-4m(c+b)(c-b)=0,化简得到a2+b2=c2.根据勾股定理的逆定理得到△ABC一定是直角三角形.
解答 (1)解:方程化为一般式得(c+b)x2-2$\sqrt{m}$ax+m(c-b)=0;
(2)证明:∵关于x的一元二次方程c(x2+m)+b(x2-m)-2$\sqrt{m}$ax=0有两个相等的实数根,
∴(-2$\sqrt{m}$a)2-4m(c+b)(c-b)=0,
∴4ma2-4m(c2-b2)=0,
∴a2+b2=c2,
∴△ABC是直角三角形.
点评 本题考查了根的判别式的应用,注意:一元二次方程ax2+bx+c=0(a、b、c为常数,a≠0),当b2-4ac>0时,方程有两个不相等的实数根;当b2-4ac=0时,方程有两个相等的实数根;当b2-4ac<0时,方程无实数根.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
6.下列各式中错误的是( )
| A. | -$\frac{7}{3}$<-2 | B. | -$\frac{3}{4}$<-$\frac{4}{5}$ | C. | |-5|<|-5$\frac{1}{2}$| | D. | 1.7>-1.7 |
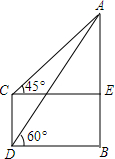 如图,某电视塔AB和楼CD的水平距离为100m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高为73.2m和楼高173.2m.(精确到0.1m)
如图,某电视塔AB和楼CD的水平距离为100m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高为73.2m和楼高173.2m.(精确到0.1m)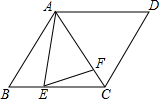 如图,在菱形ABCD中,对角线AC=AB,点E为CB边上一点(与点C不重合),点F是AC上一点.若AB=3,BE=1,∠AEF=60°,则AF的长度为$\frac{7}{3}$.
如图,在菱形ABCD中,对角线AC=AB,点E为CB边上一点(与点C不重合),点F是AC上一点.若AB=3,BE=1,∠AEF=60°,则AF的长度为$\frac{7}{3}$.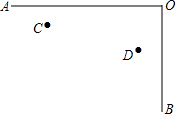 城北中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先到AO桌面上拿桔子,再到OB桌面上拿糖果,然后回到D处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短.
城北中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先到AO桌面上拿桔子,再到OB桌面上拿糖果,然后回到D处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短.