题目内容
4.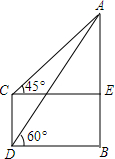 如图,某电视塔AB和楼CD的水平距离为100m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高为73.2m和楼高173.2m.(精确到0.1m)
如图,某电视塔AB和楼CD的水平距离为100m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高为73.2m和楼高173.2m.(精确到0.1m)
分析 首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形△ADB、△ACE,应利用其公共边DB=100构造等量关系式,进而可求出答案.
解答 解:设CD=xm,则
∵CE=BD=100,∠ACE=45°,
∴AE=CE•tan45°100.
∴AB=100+x.
在Rt△ADB中,
∵∠ADB=60°,∠ABD=90°,
∴tan60°=$\frac{AB}{BD}$,
∴AB=$\sqrt{3}$BD,即x+100=100$\sqrt{3}$,x=100$\sqrt{3}$-100=73.2(m),
即楼高约73.2m,塔高约173.2m.
故答案为:73.2m,173.2m.
点评 本题考查了解直角三角形的应用,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
12.一股民小江上周五买进某公司股票1000股,每股27元,下表为本周该股票涨跌情况(单位:元)
(1)星期三收盘时每股多少元?
(2)本周内最高价是每股多少元?
(3)本周内最高价每股比最低价多多少?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
(2)本周内最高价是每股多少元?
(3)本周内最高价每股比最低价多多少?
9.将方程(2x+1)2+(3x-2)-(2x-3)(x+1)=10化为一般形式是( )
| A. | x2+3x+1=0 | B. | x2+3x-2=0 | C. | x2+4x-4=0 | D. | x2+4x-2=0 |
 如图,已知:EB∥DC,∠A=∠ADE,你认为∠C和∠E相等吗?为什么?
如图,已知:EB∥DC,∠A=∠ADE,你认为∠C和∠E相等吗?为什么?