题目内容
12.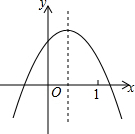 已知二次函数y=ax2+bx+c的图象如图所示,则下列选项中不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列选项中不正确的是( )| A. | a<0 | B. | c>0 | C. | 0<-$\frac{b}{2a}$<1 | D. | a+b+c<0 |
分析 由抛物线的开口方向判定a的取值范围,由抛物线于y轴的交点判定c的取值范围,根据对称轴的位置即可判定$-\frac{b}{2a}$的取值范围,由抛物线中,x=1时的函数值即可判定a+b+c的取值范围.
解答 解:A、抛物线的开口向下,∴a<0,故正确;
B、抛物线与y轴交于正半轴,∴c>0,故正确;
C、抛物线的对称轴在y轴的右边,在直线x=1的左边,∴$0<-\frac{b}{2a}<1$,故正确;
D、从图象可以看出,当x=1时,对应的函数值在x轴的上方,∴a+b+c>0,故错误.
故选D.
点评 本题主要考查二次函数的图象与系数之间的关系,熟记抛物线开口方向、对称轴、抛物线与y轴的交点等与二次函数的系数之间的关系是解决此类问题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
7.在△ABC中,∠A=45°,∠B=55°,则∠C是( )
| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
4.某商品的原价是m元,现降价30%,现价是( )
| A. | (m-30%)元 | B. | 30%m元 | C. | (1-30%)m元 | D. | (1+30%)m元 |
2.A、B两仓库分别有水泥15吨和35吨,C、D两工地分别需要水泥20吨和30吨.已知从A、B仓库到C、D工地的运价如表:
(1)若从A仓库运到C工地的水泥为x吨,则用含x的代数式表示从A仓库运到D工地的水泥为15-x吨,从B仓库将水泥运到D工地的运输费用为9x+180元;
(2)求把全部水泥从A、B两仓库运到C、D两工地的总运输费(用含x的代数式表示并化简);
(3)如果从A仓库运到C工地的水泥为10吨时,那么总运输费为多少元?
| 到C工地 | 到D工地 | |
| A仓库 | 每吨15元 | 每吨12元 |
| B仓库 | 每吨10元 | 每吨9元 |
(2)求把全部水泥从A、B两仓库运到C、D两工地的总运输费(用含x的代数式表示并化简);
(3)如果从A仓库运到C工地的水泥为10吨时,那么总运输费为多少元?
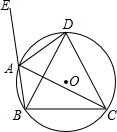 如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.
如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.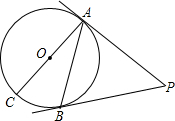 如图,AC是⊙O的直径,PA,PB是⊙O的切线,A,B为切点,∠BAC=25°.求∠P的度数.
如图,AC是⊙O的直径,PA,PB是⊙O的切线,A,B为切点,∠BAC=25°.求∠P的度数.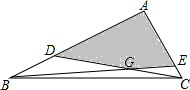 在△ABC,∠BAC=90°,AB=12cm,AC=6cm,D,E分别为AB,AC上的点,且AD=8cm,AE=5cm,连接BE,CD相交于G,则四边形ADGE的面积是$\frac{45}{2}$cm2.
在△ABC,∠BAC=90°,AB=12cm,AC=6cm,D,E分别为AB,AC上的点,且AD=8cm,AE=5cm,连接BE,CD相交于G,则四边形ADGE的面积是$\frac{45}{2}$cm2.